What is a fraction in maths?
Fractions are written in the form of ab, where a and b are integers and b can not be equal to 0.
a is called as the numerator and b as the denominator of a fraction.
A fraction is also known by other names such as common fraction, simple fraction or vulgar fraction.
45, – 712, 12
Also, a fraction is a number which represents a part of a whole. Fractions in maths helps us to measure how many parts are there and the size of each part of an object.
A fraction like 15, is read as one-fifths and it tell that one part is taken from equally divided five parts of whole.
The denominator can never be zero in a fraction.
Understand fractions with diagram
Fractions can be shown as shaded parts using shapes such as boxes or circles or any other shape. The numerator of a fraction is shown as shaded box and the denominator as the is the total number of boxes, shaded and unshaded.
In circle, it is divided into the number of sectors equal to the denominator of the fraction.These divided sectors must be equal. The number of shaded sectors are equal to the numerator of the fraction.
Fraction = numeratordenominator = shaded boxtotal number of boxes
Example 1. Fraction 12
The numerator 1 is represented by the shaded box.
The denominator 2 is the total number of boxes. 
So, the above diagram shows the 1 part out of 2 equal parts of the fraction 12.
Example 2. Fraction 13
The shaded box represents the numerator 1.
The denominator 3 is the total number of boxes. 
So, the above diagram shows the 1 part out of 3 equal parts of the fraction 13.
Example 3. Fraction 24
So, here, total number of sectors in the circle = 4
and number of shaded sectors in the circle = 2 
So, the above diagram shows the 2 parts out of 4 equal parts.
Example 4. Fraction 03
Total number of boxes = 3
and number of shaded boxes = 0 
So, the above diagram shows the 0 part out of 3 equal parts.
Example 5. Fraction 33
Total number of boxes = 3
and number of shaded boxes = 3 
So, the above diagram shows the 3 parts out of 3 equal parts.
Example 6. Fraction 410
Total number of boxes = 10
and number of shaded boxes = 4 
So, the above diagram shows the 4 parts out of 10 equal parts.
Real life example of fractions
A pizza bought from market and sharing with 8 friends equally is a real life example of fractions. The pizza is going to be divided into eight equal pieces assuming that everyone will share one equal piece.
So, a pizza has been cut into total equal pieces of 8 to divide among 8 friends. We can write the one piece of pizza in fractions as 18 , where 1 in the numerator denotes one piece and 8 in the denominator denotes the total number of pieces.
In fractions we can say one friend is sharing 18th (read as one eighth) part of pizza. As, everybody share equal piece of pizza, so we can also say everyone has shared 18 fraction of pizza.
What we have learnt about fractions from above is that a fraction has a numerator and a denominator. The denominator keeps the value of the total number of parts and numerator holds the value of a part of the whole object.
Hence, we can write in fractions 18 fraction of a whole pizza is shared to each person.
How the fraction is written, if one person is absent out of 8, eventually any one friend will get an opportunity to have 2 pieces of it. So finally we have 7 friends and 8 cut pieces of pizza.
The friend who will get 2 pieces of pizza, in fractions it can be written as 28 piece of pizza. Again, the denominator has a total number of pieces i.e. 8 and the numerator value is 2.
The remaining 6 friends share 1 piece, so their fraction of pizza shared still remains as 18.
Which are the types of fractions?
There are many types of fractions but the commonly used ten types of fractions are:
- Proper fraction
- Improper fraction
- Mixed fraction
- Unit fraction
- Decimal fraction
- Like fractions
- Unlike fractions
- Complex fraction
- Decimal fraction
1. Proper fraction
A fraction whose numerator is always less than its denominator is called proper fraction.
Proper fractions can be negative also.
712 , – 38 , 1921
2. Improper fraction
A fraction whose numerator is greater than its denominator is called improper fraction.
Improper fractions can be negative also.
115 , – 72 , 8521
A negative fraction can be checked if it is a proper or an improper fraction by taking absolute of the fraction and comparing its numerator and denominator. If numerator is less than denominator then it is a proper fraction and an improper fraction when numerator is greater than denominator.
3. Mixed fraction
A fraction which is expressed as a combination of a whole part and a proper fraction is called mixed fraction.
235 here 2 represents the whole part and 35 represents a proper fraction.
4. Unit fraction
A fraction whose numerator is one and denominator can be any positive integer is called a unit fraction.
Unit fractions are always positive.
14 , 17 , 161
In 14 , the numerator is 1 and denominator 4 which is a positive integer.
5. Decimal fraction
Fractions whose denominators are 10, 100, 1000, 10000…. and so on, are decimal fractions.
310 , – 1100 , 111000
6. Like fractions
The fractions which have the same denominator are called like fractions.
19 , 29 , 79
19 , 29 and 79 have the same denominators i.e. 9, so they are like fractions.
7. Unlike fractions
The fractions which have different denominators are called unlike fractions.
79 , 14 , 611 , 58
79 , 14 , 611 and 58 have different denominators i.e. 9, 4, 11 and 8 respectively, so they are Unlike fractions.
8. Complex fraction
A fraction whose one or both terms are also fractional numbers is called complex fraction
 2 57 ,  7  5 6 7
What is an equivalent fraction?
The equivalent fractions of a fraction are formed by multiplying its numerator and denominator by the same non zero positive number. By multiplying a fraction with a common number does not change the value of fraction.
The two fractions are said to be equivalent when multiplying numerator and denominator of one of that fraction can give the second fraction.
Example 1: Write equivalent fractions of 49
Multiply both numerator and denominator by 2:
49 × 22 = 818
Multiply both numerator and denominator by 5:
49 × 55 = 2045
∴818 and 2045 are equivalent fractions.
Example 2: Check 13 and 39 are equivalent fractions.
Multiply both numerator and denominator by 1:
13 × 11 = 13
Multiply both numerator and denominator by 2:
13 × 22 = 26
Multiply both numerator and denominator by 3:
13 × 33 = 39
∴13 becomes equal to 39 when multiplied by 3.
Hence, 13 and 39 are equivalent fractions.
Convert improper to mixed fraction
Following are the steps that can be used to convert improper fractions into mixed fractions.
Step 1: First divide the numerator by denominator of the given improper fraction.
Step 2: Write the quotient as a whole part, the remainder as numerator and the denominator will be same as is given in the improper fraction.
Convert the improper fraction 94 to mixed fraction.
Step 1: Divide the numerator 9 by the denominator 4. 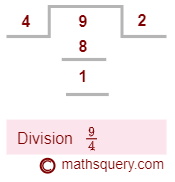
quotient = 2
remainder = 1
Step 2: Write the quotient 2 as whole part, 1 as the numerator and 4 as the denominator of the fraction part.
∴ mixed fraction = 214
Convert mixed to improper fraction
A mixed fraction always contains a whole part and a proper fraction part. Following are the steps used to convert a mixed fraction into the improper fraction.
Step 1: Multiply the whole part with the denominator of proper fraction part.
Step 2: Add numerator of the proper fraction part to the number obtained after multiplication in the step 1.
Step 3: Write a new fraction with the value of numerator is equal to the number obtained in the step 2 and the value of denominator the same as that of proper fraction.
This new fraction formed will be the required improper fraction.
Convert 345 into improper fraction.
Here, 3 is whole part and 45 is the proper fraction with 4 as numerator and 5 as the denominator.
Step 1: Multiply 3 by 5 which is equal to 15.
Step 2: Add numerator 4 of the proper fraction part to the number 15 which is obtained in the step 1, which is equal to 19.
Step 3: The new fraction with numerator equal to the number obtained in the step 2, which is 19 and denominator same as that of proper fraction, which is 5.
∴ 195 is an improper fraction.