Addition of decimal numbers
Decimals numbers are added in the same way to how the whole numbers are added. A decimal number has two parts, one is whole number part, another is the decimal part and a decimal point in between whole number and decimal parts.
To add two decimal numbers, their digits are placed one below the other and at their correct places.
The digits of whole number part are placed at the ones, tens, hundreds, thousands places and the
digits of decimal part are placed at tenths, hundredths, thousandths places.
The addition of decimal numbers always starts from the decimal part and ends at the whole number part.
The decimal point in the decimal number obtained after the addition is placed below the other
decimals points of given numbers.
Carryovers in addition of decimal numbers are handled same like how they are handles in addition of whole numbers.

Steps to add decimal numbers
Step 1: Place the digits of the whole number part of given decimal numbers at
their ones, tens, hundreds, thousands places. Also, place the digits of the decimal part
at their tenths, hundredths, thousandths places.
Step 2: Write 0 to fill the places where there are no digits written.
Step 3: Start adding the digits of decimal part first and in the direction from right to left.
Keep on adding in the same direction upto the last digit of the whole number part.
Add 0.25, 11.25 and 6.275
Step 1: Write the digits of whole number parts of 0.25, 11.25 and 6.275 under ones and tens
places.
Next, write their decimal parts digits at tenths, hundredths, thousandths places.
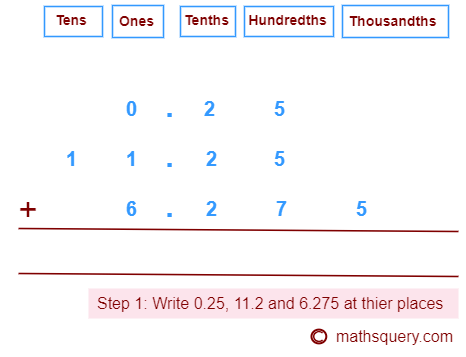
Step 2: Write 0 at the empty places as following:
0.25 to 00.250
11.25 to 11.250
6.275 to 06.275
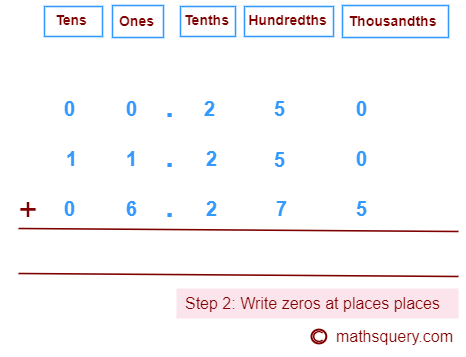
Step 3: Start adding digits starting from the thousandths place and then move to left in order of
hundredths, tenths, ones and tens places of 00.250, 11.250 and 06.275.
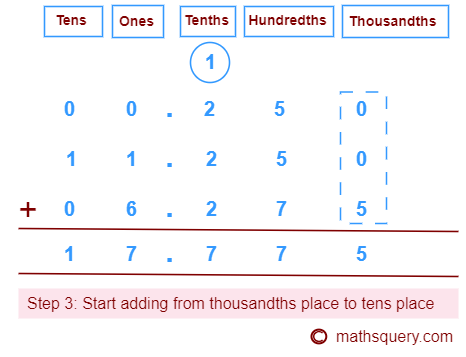
So, addition of 00.250, 11.250 and 06.275 becomes equal to 17.775.
Subtraction of decimal numbers
Decimals numbers are subtracted same like how the whole numbers are subtracted.
To subtract two decimal numbers, their digits of whole parts and decimal parts are placed at their correct
places. Subtraction also starts from the decimal part and ends at the whole number part.
Steps to subtract decimal numbers
Step 1: First write the largest number and then second number below the first. Write the
digits of the whole number part and decimal part at correct places.
Step 2: Write 0 at empty places.
Step 3: Start subtracting the digits from the decimal part and end at whole part.
Subtract 1.2 from 4.75
Step 1: 4.75 being the largest, write 1.2 below 4.75 at the correct places.
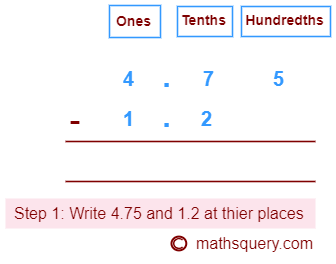
Step 2: Write 0 at the empty places.
1.2 to 1.20
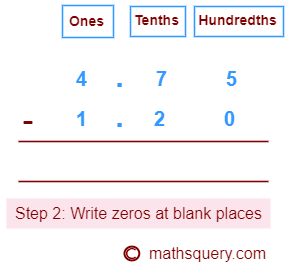
Step 3: Start subtracting the digits from the hundredths place and then move
towards the ones place of whole number parts.
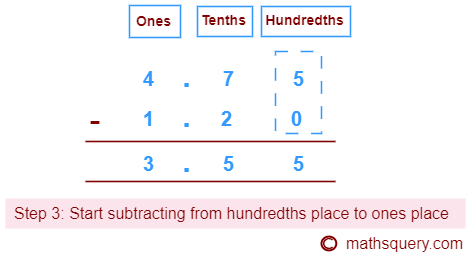
So, 3.75 is the answer of subtraction of 1.2 from 4.75.
Multiplication of decimal numbers
Multiplication of decimal numbers with any other numbers generally follows the same steps those are followed to
multiply the whole numbers.
The foremost common step for every multiplication is to write the given numbers at their right
places without using decimal points. Multiply the numbers same like the whole numbers are multiplied.
After getting an answer, the decimal point is put back to it.
Depending upon what is going to be multiplied with the decimal number, there will be different ways to
put back the decimal point in the answer, which are explained as below:
- Multiply with a whole number
- Multiply with a decimal number
- Multiply with 10
- Multiply with 100
- Multiply with 1000
1. Multiply with a whole number
In this case, the decimal point is put back in the answer after leaving the number of digits from its right side equal to the number of digits that exist after the decimal point in the given decimal number.
Multiply 21.26 with 12
Remove decimal point from 21.26 and multiply 2126 and 12
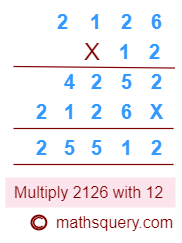
2126 × 12 = 25512
Count the number of digits after the decimal point in 21.26, which is 2.
Put the decimal point in the answer 25512 after leaving 2 digits from the right.
So, 21.26 × 12 = 255.12
2. Multiply with a decimal number
In the case of multiplying two decimal numbers, the total number of digits after the decimal points of the both given decimal numbers are counted and the decimal point is put back in the answer after leaving the same number of digits from its right side.
Multiply 11.2 with 2.3
Multiply 112 and 23
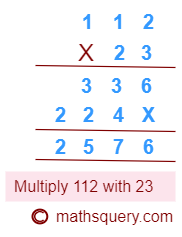
112 × 23 = 2576
The total number of digits after the decimal point in 11.2 and 2.3 are 2.
The decimal point is placed in 2576 after leaving 2 digits from the right.
So, 11.2 × 2.3 = 25.76
3. Multiply with 10
The number 10 has one zero.
To multiply, this one zero is appended after the given decimal number at the end
and the decimal point in the answer is shifted from the original position by one position to the right.
One is taken from the number of zeros in 10.
Multiply 24.72 with 10
Append one zero at the end of 24.72 and shift the decimal point by one position to the right side in
the answer.
So, 24.72 × 10 = 247.20
= 247.2
4. Multiply with 100
The number 100 has two zeros.
To multiply, the two zeros ares appended at the end of given decimal number
and the decimal point in the answer is shifted from the original position to the right by two positions.
Two is taken from the number of zeros in 100.
Multiply 125.728 with 100
Append two zeros at the end of 125.728 and shift the decimal point to the right side
by two positions.
So, 125.728 × 100 = 12572.800
= 12572.8
5. Multiply with 1000
The number 1000 has three zero.
To multiply, the three zeros are appended at the end of given decimal number
and the decimal point in the answer is shifted from the original position by three positions to the
right.
Three is taken from the number of zeros in 1000.
Multiply 2.35 with 1000
Multiply 235 and 1000
235 × 1000 = 235000
Shift the decimal point by three to the right side in the answer 235000.
So, 2.35 × 1000 = 2350.00
= 2350
Division of decimal numbers
Division of decimal numbers is performed using the long division method. In this method the number to
be divided is the dividend, which is used after removing the decimal point. The number which
will divide is the divisor. The answer of the
division in this method is taken at the end from the quotient.
In dividing the decimal numbers by a number, there are different ways to put back the decimal point in
the answer depending upon the number in divisor:
- Divisor is a whole number
- Divisor is a decimal number
- Divisor is 10
- Divisor is 100
- Divisor is 1000
1. Divisor is a whole number
If the divisor is whole number, the decimal point is placed after leaving the number of digits from right side of the answer equal to the number of digits after the decimal point in the given decimal number.
Divide 284.52 by 4
Divide 28452 after removing its decimal point by 4
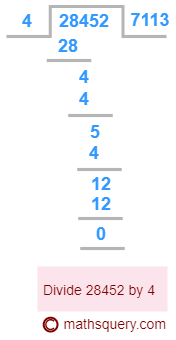
quotient = 7113
Count the number of digits after the decimal point in 284.52, which is 2.
Put the decimal point in the quotient 7113 after leaving 2 digits from the right.
28452 ÷ 4 = 71.13
2. Divisor is a decimal number
In the case, Subtract the number of digits after the decimal points of divisor from the dividend. Put the decimal point after leaving the same number of digits from the right of the quotient.
Divide 4.214 by 0.7
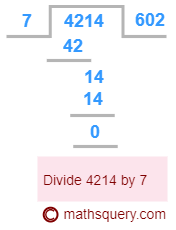
quotient = 602
Subtract the number of decimal places of 0.7 from 4.214, which 3 – 1 = 2.
Put the decimal point after leaving 2 digits from the right of the quotient 602.
4.214 ÷ 0.7 = 6.02
In the above example the number of decimal places of dividend are more than the divisor. There can be another case where the number of decimal places of dividend are lesser than the divisor. In such cases the after subtracting the number of decimal points of dividend from the divisor, put as many zeros to the right of the quotient.
Divide 98.4 by 0.24
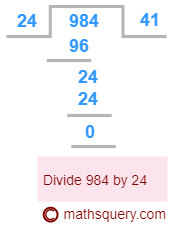
quotient = 41
Subtract the number of decimal places of 98.4 from 0.24, which 2 – 1 = 1.
Put 1 zero at the right end of the quotient 41
98.4 ÷ 0.24 = 410
3. Divisor is 10
The decimal point is shifted more towards left by one decimal place in the dividend when it is divide by 10. The one place is taken from the one zero in 10.
Divide 99.8 by 10
99.8 ÷ 10
Shift the decimal point to left by one decimal place in the dividend 99.8
So, 99.8 ÷ 10 = 9.98
4. Divisor is 100
In this case, the decimal point is shifted more towards left by two decimal places in the dividend. The two places are taken from the two zeros in 100.
Divide 784.2 by 100
784.2 ÷ 100
Shift the decimal point to left by two decimal places in the dividend 784.2
So, 784.2 ÷ 100 = 7.842
5. Divisor is 1000
In division by 1000, the decimal point is shifted towards left by three decimal places in the dividend again. The three places are taken from the three zeros in 1000.
Divide 164.5 by 1000
164.5 ÷ 1000
Shift the decimal point to left by three decimal places in the dividend 164.8
So, 164.5 ÷ 1000 = 0.1645







