What is LCM & Multiples of Number? Methods to Find LCM

Introduction

LCM (Least Common Multiple or Lowest Common Multiple), they all are the same terms. We use them while finding out the number which is the lowest common multiple among many multiples of a number.
To see in more detail how it is calculated, first of all, let’s review some general terms related to LCM.

Multiple of a number

A multiple is a number that we can get from a number when multiplied by any positive integer.

Example

What are the multiples of 7?
We can say there are unlimited multiples of 7.

To be short, 14 is a multiple of 7.
Why?
Because, here, 7 is the number
when 7 is multiplied by 2, the obtained number 14 is multiple 7.
How?
7 × 2 = 14
Still, we can create more multiples of 7 by multiplying 7 with positive integers such as 3, 4, 5, 6, 7, 8….. and so on
7 × 3 = 21
7 × 4 = 28
7 × 5 = 35
7 × 6 = 42
7 × 7 = 49
7 × 8 = 56
So, here, 21, 28, 35, 42, 49, 56 are also multiples of 7.

Common multiples of numbers

Common multiples are calculated for two or more than two numbers. They are the multiples which are common among the multiples of the given numbers.

Example

Let’s understand it by taking the two numbers as 2 and 4 to find their common multiples.
Step1: find out the multiples of 2 and 4 separately.

Multiples of 2:
2 × 1 = 2
2 × 2 = 4
2 × 3 = 6
2 × 4 = 8
2 × 5 = 10
2 × 6 = 12
The multiples of 2 are 2, 4, 6, 8, 10, 12 and so on.
Multiples of 4:
4 × 1 = 4
4 × 2 = 8
4 × 3 = 12
4 × 4 = 16
4 × 5 = 20
4 × 6 = 24
The multiples of 4 are 4, 8, 12, 16, 20, 24 and so on.
Step2: Find out the common multiples of 2 and 4.
Finally, we can say 4, 8, 12 are the common multiples of 2 and 4, because the multiples 4, 8 and 12 do exist for both numbers 2 and 4.

What is LCM and methods to find it

LCM (Least Common Multiple or Lowest Common Multiple) is the smallest number among the common multiples of given numbers.

There are three methods to find the least common multiple.

Common multiple method
Prime factorization method
Common division method

Let’s learn them next with examples.

1. Common multiple method

This method calculates LCM from the smallest common multiple of given numbers.

Steps to find LCM using common multiple method

Step 1: Find out the multiples of each of the given numbers.
Step 2: Find out the common multiples from from each number calculated in step 1.
Step 3: Find out the smallest number among those common multiples

Example

Find the LCM of 2 and 4 using common multiple method.
Step 1: Find out the multiples of 2 and 4.
Multiples of 2
2 × 1 = 2
2 × 2 = 4
2 × 3 = 6
2 × 4 = 8
2 × 5 = 10
2 × 6 = 12
The multiples of 2 are 2, 4, 6, 8, 10, 12 and so on.
Multiples of 4
4 × 1 = 4
4 × 2 = 8
4 × 3 = 12
4 × 4 = 16
4 × 5 = 20
4 × 6 = 24
The multiples of 4 are 4, 8, 12, 16, 20, 24 and so on.
Step 2: Find out the common multiples of 2 and 4.
Therefore, the common multiples are 4, 8 and 12.
Step 3: Find out the smallest number among those common multiples, that would be the LCM of 2 and 4.
Therefore, the smallest number among common multiples 4, 8 and 12 is 4.
Hence, LCM of 2 and 4 is 4.

2. Prime factorization method

This method calculates LCM from the product of the maximum number of times the prime factors of given numbers occurs.

Steps to find LCM using prime factorization method

Step 1: Split each given number into its prime factors.
Step 2: Write prime factors of each number with maximum number of times they occur.
Step 3: Multiply all prime factors from step 2, which will be the LCM.

Example

Example 1: Find the LCM of 12 and 20 using prime factorization method.
Step 1: Split 12 and 20 into its prime factors
Prime factors of 12
12 = 2 × 2 × 3 = 2² × 3¹
Prime factors of 20
20 = 2 × 2 × 5 = 2² × 5¹
Step 2: Write prime factors 2, 3 and 5 with maximum number of times they occur.
Common prime factors with maximum number of times it occurs are 2², 3¹ and 5¹
Step 3: Multiply all prime factors from step 2, which will be the LCM.
2² × 3¹ × 5¹ = 60
Hence, LCM of 12 and 20 is 60.

Example 2: Find the LCM of 18 and 24 using prime factorization method.
Step 1: Split 18 and 24 into its prime factors
Prime factors of 18
12 = 2 × 3 × 3 = 2¹ × 3²
Prime factors of 24
24 = 2 × 2 × 2 × 3 = 2³ × 3¹
Step 2: Prime factors 2 and 3 with maximum number of times they occur are 2³ and 3²
Step 3: Multiply all prime factors.
2³ × 3² = 72
Hence, LCM of 18 and 24 is 72.

3. Common division method

This method calculates LCM from the product of the divisors which divide the given numbers exactly.

Steps to find LCM using common division method

Step 1: Write the given numbers in a row and separate them using hyphen (-).
Step 2: Divide these numbers by a number which can divide at least two of the given numbers exactly and write down their quotients just below them. Write the numbers as it is which are not divisible. Repeat the step 2 until two of the given numbers are divisible by the same number.
Step 3: Multiply all divisors and the undivided numbers which are left in the last row, which will be the LCM of given numbers.

Example

Example 1: Find the LCM of 12 and 20 using common division method.
Step 1: Write 12 and 20 in a row and separate them using hyphen (-).

Step 2: Divide 12 and 20 by a number which can divide at least two of the given numbers exactly, which can be 2. Write 6 and 10 below 12 and 20 respectively as shown in the figure below.
Find the LCM of 12 and 20 using common division method - step 2
Repeat the same process. Divide 6 and 10 by 2, which gives 3 and 5.
3 and 5 can not be divided further by any same number.

Step 3: Multiply all divisors i.e. 2, 2 and the undivided numbers i.e. 3, 5 which are left in the last row.
2 × 2 × 3 × 5 = 60
∴ LCM of 12 and 20 is 60.

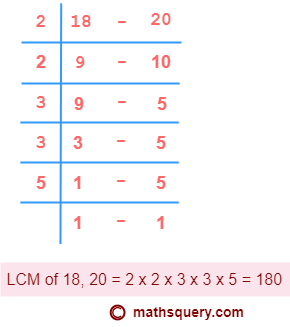
Example 2: Find the LCM of 18 and 24 using common division method.
Step 1: Write 18 and 24 in a row and separate them using hyphen (-).

Step 2: Divide 18 and 24 by a number which can divide at least two of the given numbers exactly, which can be 2. Write 9 and 12 below 18 and 24 respectively as shown in the figure below.
Find the LCM of 18 and 24 using common division method - step 1
Repeat the same process. Divide 9 and 12 by 3, which gives 3 and 4.
3 and 4 can not be divided further by any same number.

Step 3: Multiply all divisors i.e. 2, 3 and the undivided numbers i.e. 3, 4 which are left in the last row.
2 × 3 × 3 × 4 = 72
∴ LCM of 18 and 24 is 72.

Four properties of LCM

Property 1

The LCM of two or more co-prime numbers is equal to their product.

Example

Example 1: LCM of 2 and 3 is 2 × 3 = 6, because 2 and 3 are co-prime numbers.

Example 2: LCM of 10 and 11 is 10 × 11 = 6, because 10 and 11 are co-prime numbers.

Property 2

If one number is multiple of another number then LCM is the greatest number among the two given numbers.

Example

Example 1: LCM of 18 and 9 is 18, because 18 is multiple of 9.

Example 2: LCM of 18 and 54 is 54, because 54 is multiple of 18.

Property 3

LCM of two or more prime numbers is equal to their product.

Example

Example 1: LCM of 5 and 11 is 5 × 11 = 55, because 5 and 11 are prime numbers.

Example 2: LCM of 3, 11 and 13 is 3 × 11 × 13 = 429, because 3, 11 and 13 are prime numbers.

Property 4

The LCM is not less than any of the given numbers.

Example

Example 1: LCM of 6 and 8 is 24, which is greater than the given numbers 6 and 8.

Example 2: LCM of 3 and 10 is 30, which is greater than the given numbers 3 and 10.

Relationship between LCM and HCF

The LCM and HCF are related to each other using a formula which can be used to find any of the one value i.e. LCM or HCF of given numbers, if value of one is known.

Product of LCM and HCF of given numbers is equal to the product of the numbers.

Formula

LCM × HCF of two numbers = Product of the two numbers

Frequently Asked Questions

1) What is LCM?

LCM stands for Least Common Multiple or Lowest Common Multiple. It is the smallest number that is obtained from the common multiples of given number.

2) What are the methods to find LCM?

1) Prime factor method
2) Common division method
3) Common multiple method

3) What is the relationship between HCF and LCM?

For any numbers a and b: Product of their LCM and HCF = Product of the numbers

Solved Examples

1) Find LCM of 12 and 24.

We can find LCM by common multiple method
Multiples of 12 are 12, 24, 36, 48, 60.
Multiples of 24 are 24, 48, 72, 96, 120.
From the above, the common multiples are 24, 48 and the lowest number of multiple is 24.
Therefore, LCM of 12 and 24 is 24.

2) Find LCM of 18 and 20 using prime factorization method.

Prime factorization of 18 = 2 × 3 × 3 = 2 × 3²
Prime factorization of 20 = 2 × 2 × 5 = 2² × 5¹
From the above, common factors = 2.
To find the LCM, we take the highest power of common factor i.e. 2²
∴ LCM of 18 and 20 = 2² × 3² × 5¹
= 4 × 9 × 5
= 180

3) Find LCM of 18 and 20 using common division method.

LCM of 18 and 20 using division method
LCM = 2 × 2 × 3 × 3 × 5
LCM = 4 × 9 × 5
= 180

4) Find LCM of 18 and 20 using common multiple method.

Multiples of 18 = 18, 36, 54, 72, 90, 108, 126, 144, 162, 180
Multiples of 20 = 20, 40, 60, 80, 100, 120, 140, 160, 180, 200
Common multiple = 180
∴ LCM of 18 and 20 = 180

5) If two numbers are in the ratio 9:10 and their HCF is 2. Find their LCM.

Let the numbers are 9x and 10x.
where HCF = x = 2
∴ LCM = 9 × 10 × x
LCM = 90x
or LCM = 90 × 2 = 180

6) Three numbers are in the ratio 2:3:4 and their LCM is 120. Find their HCF.

Let the numbers are 2x, 3x and 4x.
where HCF = x
∴ LCM = 2² × 3 × x
LCM = 4 × 3 × x = 12x
But, LCM = 120 (..............given)
or 12x = 120
x = 10

Fill in Blanks Worksheet

Type:	Blanks
Count:	1

The fourth multiple of 15 is ___________.
The ___________ of two prime numbers is equal to their product.
The product of ___________ and LCM is equal to the product of their given numbers.
The LCM of 7 and 13 is ___________.
The LCM of 4 and 12 is ___________.
The eighth multiple of 18 is ___________.
HCF of 5 and 8 is 1 and the product of 5 and 8 is 40, then the value of LCM is ___________.
The LCM of two coprime numbers is equal to their ___________.
If two numbers are in the ratio 2:3 and their HCF is 5, then the LCM of two numbers will be ___________.
Every number is ___________ of itself.