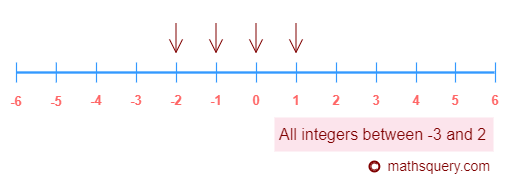
What are integers?
Integers are collection of positive 1, 2, 3, 4, 5, 6, …. and negative -1, -2, -3, -4, -5, -6,….. natural numbers including a zero. In terms of whole numbers they are positive and negative of whole numbers because 0 is already included in whole numbers.
Negative numbers are considered as less than 0. They are read, for example -1 as minus one.
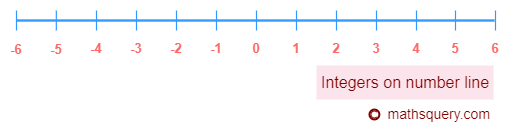
Representation on number line
Integers can be represented on a number line as shown in the figure below. The negative numbers lie on left
side of 0 and positive numbers lie on the right side of 0.
The numbers lying on the right side of 0 are called positive integers.
The numbers lying on the left side of 0 are called negative integers.
The numbers without any sign i.e. + or -, are considered as positive integers.
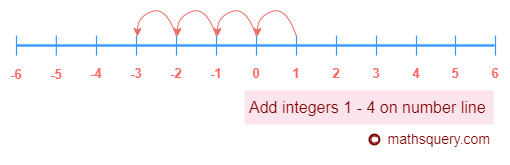
The integers can also be operated with basic arithmetic operations like addition, subtraction, multiplication and division.
Addition operation
To add integers there are some following rules those need to be followed.
Both positive
Two positive integers are added same like the whole numbers are added.
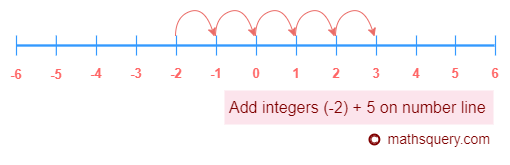
(6) + (4)
6 + 4 = 10
Both negative
To add two negative integers, first they are changed into their absolute values. Then, add the numbers like whole numbers are added. After adding, put a sign of minus before the answer obtained.
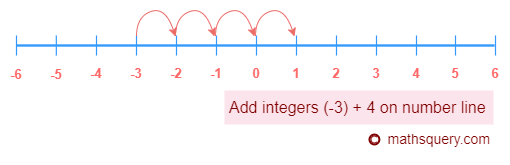
(-6) + (-4)
Absolute values of (-6) and (-4) are 6 and 4 respectively
Add 6 and 4. 6 + 4 = 10
Put a minus sign before 10, which is -10
∴ (-6) + (-4) = -10
Two signs can be written together by only using brackets in between them.
e.g. -(-6), 3 + (-2), 7 – (-2)
Positive and negative
To add a positive and a negative integers, first they are changed into their absolute values. Then, the absolutes of smaller number is subtracted from larger number instead of addition. In the final answer, put a sign before it of the larger number in the problem.
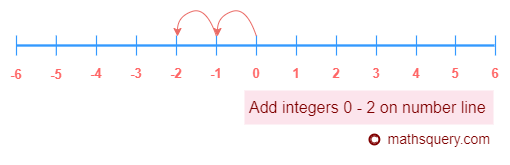
(6) + (-4)
Absolute values of (6) and (-4) are 6 and 4 respectively
Subtract absolute of smaller number 4 from 6
i.e. 6 – 4 = 2
2 will have sign of the larger number 6 i.e. no sign or positive
∴ (6) + (-4) = 2
Subtraction operation
Subtraction of integers involves subtracting of one integer from another but the final result depends upon the sign of the integers.
Positive from positive
Subtraction of two integers is carried out in the same way as the two whole numbers are subtracted. Small
integer will be subtracted from the larger integer. The answer of the subtraction will have
– sign if a larger number is being subtracted from smaller number
and + or no sign if smaller number is being subtracted from larger number.
Subtract 16 from 10
i.e. (10) – (16) = ?
To get the answer, smaller number 10 will be subtracted from the largest number 16
i.e. 16 – 10 = 6
The answer 6 will have sign of – because larger number 16 is being subtracted from the smallest
number 10 in the problem statement.
∴ (10) – (16) = -6
Subtract 10 from 16
i.e. (16) – (10) = ?
Subtract smaller number 10 from the largest number 16
i.e. 16 – 10 = 6
6 will have sign of + because 10 is being subtracted from 16 in the problem statement.
∴ (16) – (10) = 6
Change the sign to + if there is – outside the bracket.
i.e. -(-2) becomes +2 or can be written as simply 2
Negative from negative
While subtracting two negative integers, sign before the second negative integer being subtracted is changed. It always changes from – to +. After changing the signs, the two numbers are in opposite signs and hence can be subtracted normally by subtracting smaller number from the larger number and the final answer will have sign of the larger number.
Subtract -17 from -11
i.e. (-11) – (-17) = ?
Change the sign of the second number being subtracted from – to +
(-11) – (-17) = -11 + 17
Subtract 11 from 17
-11 + 17 = 17 – 11 = 6
The sign of 6 will be same as that of the largest number 17, which is + or no need to write +
Subtract -18 from -20
i.e. (-20) – (-18) = ?
= -20 + 18
= -2
The sign of 2 will have the same sign as of 20, which is –
Positive from negative or vice versa
When there is one positive and another is negative integer in the subtraction, then change the sign in between two integers There will be two cases depending upon whether the second integer being subtracted is positive or negative.
-
first positive and second negative
In case of first positive and second negative integers, then change the sign from – to + before the bracket and remove the – sign inside the bracket. Both numbers will get added up and the final answer will have + sign. -
first negative and second positive
When first integer is negative and second is positive, then add the absolute values of both numbers and put the sign of – in the final answer.
Subtract 15 from -20
i.e. -20 – (15) = ?
Change – before bracket to + and -20 to 20
= 15 + 15 = 35
35 will keep the sign of the larger number 20, i.e. +
Subtract -15 from 20
i.e. 20 – (-15) = ?
Change – before bracket to + and change negative integer -15 to the positive integer 15
= 20 + 15 = 35
35 will keep the sign of the larger number 20, i.e. +
Multiply operation
Multiplication on integers is also performed same as that of two whole numbers.
Positive with negative
If one is positive and another is negative integer, they are multiplied with their absolute values and the sign of – is used in the final answer.
Multiply -6 by 8
i.e. (-6) × 8 = ?
Multiply absolute values of -6 and 8 i.e. 6 × 8 = 48
Add – sign to 48
∴ (-6) × 8 = -48
Negative with negative
Absolute values of both negative integers are multiplied and a + sign is put in the final answer.
Multiply -6 by -8
i.e. (-6) × (-8) = ?
Multiply absolute values of -6 and -8 i.e. 6 × 8 = 48
Add + sign to 48
∴ (-6) × (-8) = 48
Positive with positive
Two positive integers are multiplied same as that of two whole numbers. Final answer is written with + sign.
Multiply 6 by 8
i.e. 6 × 8 = ?
simply multiply 6 and 8
∴ 6 × 8 = 48
Divide operation
Division on integers is same as that of multiplying whole numbers.
Positive by negative or vice versa
Divide the absolutes of positive and negative integers and lastly put the – sign in the answer.
Divide -48 by 6
i.e. (-48) ÷ 6 = ?
Divide their absolutes 48 and 6 i.e. 48 × 6 = 8
Put – sign to 8
∴ (-48) × 6 = -8
Either both positive or negative
If both numbers are positive or are negative integers, then again their absolutes are divided with + sign in the final answer.
Divide 48 by 6
i.e. 48 ÷ 6 = ?
∴ 48 × 6 = 8
Divide -48 by -6
i.e. (-48) ÷ (-6) = ?
Divide absolutes 48 × 6 = 8
∴ (-48) × (-6) = 8