Circumference of circle
Circumference is the length of the boundary of the circle.
Its units are same as that of length i.e meter, centimeter, millimeter etc.
In the figure below the boundary of the circle is marked with “Circumference”.
The circumference of a circle with radius r can be calculated by multiplying diameter with the constant π.
As diameter of a circle is double of its radius. So, the formula used to find circumference is 2 π r.
where, r is radius of circle and π is a constant value.
The value of π =
22
7
or 3.14
Circumference of circle = 2 π r
Area of circle
Area of circle is a measure of space of the surface of circle. Its units are same as that of area
i.e meter2,
centimeter2, millimeter2 etc.
In the figure below the shaded part inside the circle denotes the area of the circle.

The area of a circle with radius r can be calculated using the formula π r2.
where, π is the constant value and r is radius of the circle.
Area of circle = π r2
Area of sector or minor sector
Area of sector of a circle is the region of the circle that is bounded by an arc and two radii of the circle.
In the figure below the shaded part inside the circle denotes the area of the sector of the circle,
formed by two radii which make an angle θ at the centre of circle (called as central angle) and the
opposite minor arc.
Area of sector is always assumed as the area of minor sector area if “minor” is not mentioned.
Area of minor sector of circle =
θ
360
× π r2
where θ is the central angle in degrees.
Area of minor sector of circle =
θ
2 π
× π r2
where θ is the central angle in radians.
Area of minor sector of circle when length of arc is given =
r l
2
where r is radius and l is length of arc.
Sector area with Unitary method
Area formula of minor sector of circle is
θ
360
× π r2.
This formula can be derived using the Unitary method here as under.
In the above diagram of “Area of circle”, the area of circle π r2 covers the full circle. This
whole
area is covered by a sector whose two radii coincides each other and make the central angle θ = 360°.
By applying Unitary method, it can be written as:
Central angle of 360° covers the area of circle = π r2
Central angle of 1° covers the area of circle =
π r2
360°
Central angle of θ covers the area of circle =
π r2
360°
× θ
∴ area of sector of circle with central angle θ =
π r2
360°
× θ
=
θ
360°
× π r2
As we know 360° in radians can be written as 2 π radians
∴ the area of sector in radians =
θ
2 π
× π r2
Similarly, Unitary method can be applied to derive formula in terms of radius r and length of arc l.
The whole area of circle is covered by an arc whose length is equal to the circumference of the circle.
Using Unitary method, it can also be written as:
Length of arc 2 π r covers the area of circle = π r2
Length of arc 1 covers the area of circle =
π r2
2 π r
Length of arc l covers the area of circle =
π r2
2 π r
× l
=
r l
2
∴ area of sector of circle with arc of length l =
r l
2
Depending upon the measure of the angle the sectors of the circle are known by following names:
| Central angle of sector | Name of sector |
|---|---|
| 90° | Quadrants |
| 60° | Sextants |
| 45° | Octants |
Area of major sector
Area of major sector is the area left other than the area of minor sector of circle.
The figure below shows the area of major sector with the shaded part
formed by two radii which make a central angle of θ in minor sector and the opposite major arc.
It is calculated by subtracting the area of minor sector from the total area of the circle.
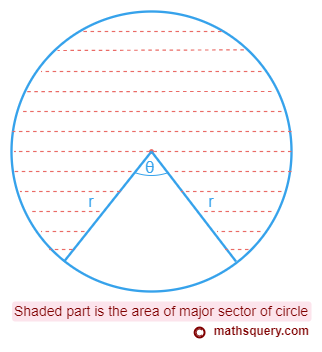
Area of major sector =
(360 – θ)
360
× π r2
where θ is the central angle in minor sector in degrees.
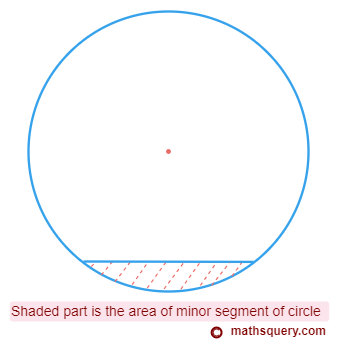
Area of minor segment
Area of minor segment is the region enclosed between a minor arc and the chord.
The figure below shows the area of minor segment with the shaded part.
Formula to find area of segment
In the below diagram, the shaded part below the chord AB is the area of the minor segment.
OA and OB are the two radii of length r. θ is the central angle.
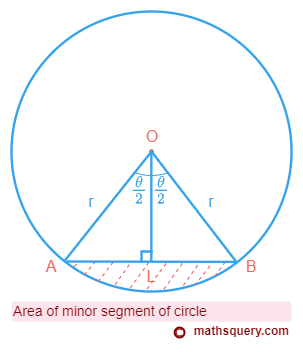
So, Area of minor segment = area of minor sector – area of ΔAOB
Area of minor sector =
θ
360°
× π r2
To calculate the area of ΔAOB, follow the steps below.
Area of ΔAOB = 12
× AB × OL
In ΔAOL
AL
OA
=
Sin
θ
2
AL
r
=
Sin
θ
2
AL =
r Sin
θ
2
AB = 2 × AL
∴ AB = 2 × r Sin
θ
2
= 2 r Sin
θ
2
Also,
OL
OB
=
Cos
θ
2
OL
r
=
Cos
θ
2
OL =
r Cos
θ
2
∴ Area of ΔAOB = 12
× 2 r Sin
θ
2
× r Cos
θ
2
= r2 Sin
θ
2
× r Cos
θ
2
Again, Area of minor segment = area of minor sector – area of ΔAOB
=
θ
360°
× π r2 –
r2 Sin
θ
2
× r Cos
θ
2
= r2 [
θ
360
× π –
Sin
θ
2
Cos
θ
2
]
Area of minor segment = r2 [ θ 360 × π – Sin θ 2 Cos θ 2 ]
Area of major segment
Area of major segment is the region enclosed between a major arc and the chord.
The figure below shows the area of major segment with the shaded part.
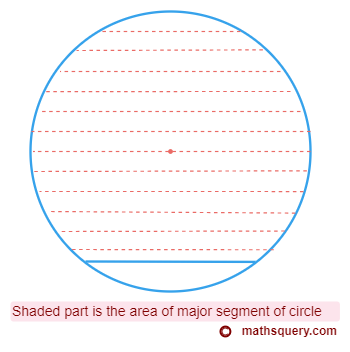
Area of major segment = π r2 – Area of minor segment
Length of arc
The length of arc is the distance between two points on the boundary of a circle.
The figure below shows the area of major segment with the shaded part.
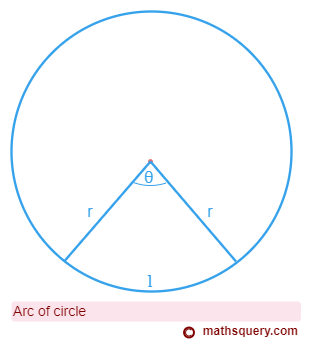
Length of arc (in degrees) =
θ
360
× 2 π r
Length of arc (in radians) = θ r
Circumference of semi circle
Semi circle is a half part of a circle divided into two equal parts by the diameter.
The circumference of semi circle is the length of its curved path. This length becomes equal to the half
of circumference of the circle.
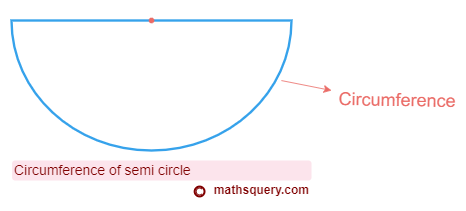
The circumference of a semi circle with radius r can be calculated by doing half of the Circumference of circle 2 π r 2 , which becomes π r.
Circumference of semi circle = π r
Perimeter of semi circle
Perimeter of semi circle is the total length of it boundary, which is equal to sum of its circumference and diameter.
Perimeter of semi circle = π r + D,
where r is radius of semi circle and D is its diameter
Area of semi circle
The Area of semi circle is half of the area of the circle.
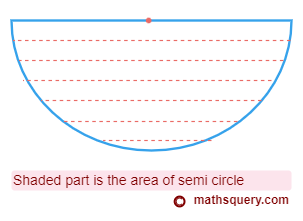
The area of a semi circle with radius r can be calculated by doing half of the area of circle as π r2 2
Circumference of semi circle = π r2 2