Introduction
Quadrilateral is one of the type of polygons, which we already studied in the chapter
Curve, Polygon and Types of Polygon. From this chapter, we can
recall that a quadrilateral is a polygon which has four sides and four interior angles.
In this chapter, we will learn in detail about the
quadrilateral
about its sides, diagonals. angles and its different types.
Definition
Quadrilateral is a plane closed figure formed by joining four line segments. It is a polygon with four sides. Quadrilateral has four sides, four vertices and four angles.

In the above figure, ABCD is quadrilateral with four line segments AB, BC, CD and DA. AB, BC, CD and DA are called sides of Quadrilateral ABCD. Also, A, B, C and D are called vertices of quadrilateral.
Quadrilateral ABCD has four angles viz. ∠DAB, ∠ABC, ∠BCD and ∠CDA. We can write these angles as ∠A, ∠B, ∠C and ∠D respectively.
Adjacent Sides of a quadrilateral
Two sides of a quadrilateral are said to be adjacent sides if they meet at a common end point. In above figure, AB and BC are adjacent sides of the quadrilateral ABCD because they have a common end point B. Also, BC and CD are adjacent sides of the quadrilateral ABCD because they have common end point C. CD and DA are adjacent sides of the quadrilateral ABCD because they have common end point D. DA and AB are also the adjacent sides of the quadrilateral ABCD because they have common end point A.
Opposite Sides of a quadrilateral
The sides of a quadrilateral are called as opposite sides if they do not have a common end point. Again, referring to the above quadrilateral ABCD, AB and CD are the opposite sides because they have no common end point. Also, AD and BC are also the opposite sides of the quadrilateral ABCD because they also have no common end point.
Diagonals of a quadrilateral
The line segment which joins the opposite vertices of a quadrilateral is called its diagonal.

In the above quadrilateral ABCD, AC and BD are two diagonals of quadrilateral.
Why?
Because the AC line segment joins two opposite vertices A and C and hence AC is a diagonal of quadrilateral ABCD. Similarly, BD line segment joins two opposite vertices B and D, that makes BD the diagonal of quadrilateral ABCD.
Which are types of quadrilateral?
As the number of sides of a quadrilateral are always fixed i.e. four, so, the types of Quadrilateral are
classified based on how the length of four sides vary and how inclined the sides are.
Let’s have a look at very common types of a quadrilateral.
Parallelogram
A quadrilateral, in which both pairs of opposite sides are parallel, is called parallelogram. Also, opposite sides of a parallelogram are equal.

In above figure, ABCD is a parallelogram because opposite sides AB and CD are parallel to each other and have
equal length. Also, AD and BC are parallel to each other and have equal length. Or, we can write them as:
AB = CD and AB || CD. Also, AD = BC and AD || BC
Hence, the above ABCD quadrilateral is a parallelogram.
A diagonal of parallelogram divides it into two congruent triangles and the two diagonals of a parallelogram bisect each other.

In above parallelogram ABCD, the two diagonals AC and BD bisect each other at O. Therefore, OA=OC and OB=OD.
Rectangle
A quadrilateral in which both pairs of opposite sides are parallel, equal in length and each of four angles is of 90°, is called rectangle.

In given figure, ABCD is a rectangle. Because, the opposite sides are parallel, i.e. AB||CD and BC||AD.
Secondly, the length of opposite sides are equal, i.e. AB = CD and BC = AD. And the last, all of four angles are
of 90°, i.e.
∠A = 90°, ∠B = 90°, ∠C = 90°, ∠D = 90°
Diagonals of rectangle are always equal in length and bisect each other.

In the above figure, AC = BD, because the diagonals of a rectangle are equal in length. And OA = OC and OB = OD, because diagonals of a rectangle bisects each other.
Square
A quadrilateral in which all sides are parallel, equal and each of its angle is 90 degree, is called square.

In above figure, ABCD is a square because AB || CD, BC || AD and AB = BC = CD = DA. ∠A = 90°,
∠B = 90°, ∠C = 90° and ∠D = 90°.
The diagonals of a square are equal in length and bisect each other at right angle.

In above figure, AC and BD are diagonals of the square ABCD and intersect each other at O. Both diagonals are
equal in length. i.e. AC = BD.
Both diagonals bisect each other. i.e. OA = OC and OB = OD
Both diagonals intersect each other at right angle. i.e. ∠AOB = ∠BOC = ∠COD =
∠AOD = 90°
Rhombus
A quadrilateral in which both pairs of opposite sides are parallel and all four sides are equal in length, is called rhombus. Rhombus is also called as equilateral quadrilateral.

In above figure, ABCD is a rhombus because AB || CD, BC || AD and AB = BC = CD = DA. The diagonals of a rhombus bisect each other at right angle.

In the above figure, the diagonals AC and BD bisect each other at right angle. i.e. OA = OC and OB = OD. ∠AOB = ∠BOC = ∠COD = ∠AOD = 90°

Also, in above figure, diagonals of a rhombus bisect the angles of rhombus at vertices. i.e. ∠1 = ∠2, ∠3 = ∠4, ∠5 = ∠6 and ∠7 = ∠8
Trapezium
A quadrilateral in which only one pair of opposite sides are parallel, is called trapezium.

In above figure, ABCD is a trapezium because AB || CD and AD and BC are non parallel sides.
Isosceles Trapezium
If two non parallel sides of trapezium are equal, it is called isosceles trapezium.

In above isosceles trapezium ABCD, AB || CD and non parallel sides BC and AD are equal in length, i.e. BC = AD.
In isosceles trapezium, base angles are of equal magnitude. i.e. ∠A = ∠B and
∠C = ∠D
In isosceles trapezium, diagonals are equal in length. i.e. AC = BD.
Kite
A quadrilateral in which two pairs of adjacent sides are equal, is called kite.

In the above figure, ABCD is a kite because AB = BC and CD = DA.
Frequently Asked Questions
1) What is quadrilateral?
Quadrilateral is a plane figure which is formed by joining four line segments.
2) How many angles does a quadrilateral have?
A quadrilateral has four angles.
3) How many vertices does a quadrilateral have?
A quadrilateral has four vertices.
4) What is the sum of four angles of a quadrilateral?
Sum of four angles of a quadrilateral is 3600
5) How many diagonals does a quadrilateral have?
There are two diagonals in a quadrilateral.
Solved Examples
1) In a parallelogram, ABCD if ∠A = 600, find the other three angles.

Solution
given ∠A = 600
∴ ∠C = 600
∵ ∠A and ∠C are opposite angles of parallelogram.
∠A + ∠B = 1800
∵ adjacent angles in parallelogram are supplementary.
600 + ∠B = 1800
∠B = 1800 - 600
∠B = 1200
∴ ∠D = 1200
∵ ∠B and ∠D are opposite angles of parallelogram.
2) Angles of quadrilateral are 900, 800 and 1100. Find the fourth angle
Solution
Let fourth angle of quadrilateral be x.
x + 900 + 800 + 1100 = 3600 (∵ Sum of angles of
quadrilateral is 3600.)
x + 2800 = 3600
x = 3600 - 2800
x = 800
3) In rhombus PQRS, if ∠P = 700. Find the ∠Q, ∠R and ∠S.

Solution
∠P = 700
Also, ∠R = ∠P (∵ opposite angles of rhombus are equal)
∴ ∠R = 700
∠P + ∠Q = 1800 (∵ Sum of adjacent angles is 1800.)
700 + ∠Q = 1800
∠Q = 1800 - 700
∠Q = 1100
Also, ∠S = ∠Q (∵ opposite angles of rhombus are equal)
∴ ∠S = 1100
4) If two adjacent angles ∠A and ∠B of parallelogram ABCD are equal. Find all four angles of the parallelogram.
Solution
In parallelogram ABCD, ∠A and ∠B are adjacent angles.
Let ∠A = ∠B = x°
∴ ∠A + ∠B = 180° (∵ sum of adjacent angles of ||gm is 180°)
∴ x + x = 180°
2x = 180°
x = 90°
∴ ∠A = ∠B = 90°
Also, ∠A = ∠C (∵ diagonally opposite angles of ||gm are equal)
∠C = 90°
Also, ∠B = ∠D (∵ diagonally opposite angles of ||gm are equal)
∠D = 90°
5) Two adjacent angles ∠P and ∠Q of a parallelogram PQRS are in the ratio of 4 : 5. Find the ∠P and ∠Q.
Solution
∠P : ∠Q = 4 : 5
or it can be written as ∠P = 4x, ∠Q = 5x
Since adjacent interior angles are supplementary
∴ ∠P + ∠Q = 180°
4x + 5x = 180°
9x = 180°
x = 20°
∴ ∠P = 4x = 4 × 20 = 80°
∠Q = 5x = 5 × 20 = 100°
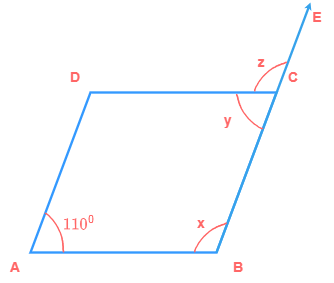
6) In a parallelogram ABCD ∠A = 110°. Find the values of x, y and z.
Solution
∠A = ∠BCD (∵ diagonally opposite angles of ||gm are equal)
∴ ∠BCD = 110° (∵ ∠A = 110°)
∴ y = ∠BCD = 110°
Also. ∠A + ∠B = 180° (∵ adjacent angles of ||gm are supplementary)
∴ ∠A + x = 180°
110° + = 180°
x = 180° - 110°
x = 70°
Also. ∠DCB + ∠DCE = 180° (∵ ∠DCB and ∠DCE form linear pair of angles)
∴ y + z = 180°
110° + z = 180°
z = 180° - 110°
z = 70°
7) In the parallelogram ABCD, find the values of x, y and z.

Solution
∠ADC = ∠ABC (∵ diagonally opposite angles of ||gm are equal)
∴ z = 110°
Also. ∠A and ∠B are adjacent angles of ||gm ABCD
∴ ∠A + ∠B = 180° (∵ adjacent angles of ||gm are supplementary)
(x + 30°) + 110° = 180°
x + 140° = 180°
x = 180° - 140°
z = 40°
In ΔABC
∠BCE = ∠BAC + ∠ABC (∵ exterior angle of a triangle is equal to sum of its
opposite interior angles)
y = 110° + 30°
y = 140°
8) In quadrilateral PQRS, the four angles are in the ratio of 1 : 2 : 3 : 4. Find the value of all the four angles.

Solution
Since ∠P, ∠Q, ∠R and ∠S are in the ratio of 1 : 2 : 3 : 4
Let ∠P = x, ∠Q = 2x, ∠R = 3x and ∠S = 4x
∴ ∠P + ∠Q + ∠R + ∠S = 360°
or x + 2x + 3x + 4x = 360°
10x = 360°
x = 36°
∴ ∠P = x = 36°
∠Q = 2x = 2 × 36° = 72°
∠R = 3x = 3 × 36° = 108°
∠S = 4x = 4 × 36° = 144°
Fill in Blanks Worksheet
| Type: | Blanks |
| Count: | 1 |
- A quadrilateral has ___________ vertices.
- A trapezium is a quadrilateral in which one pair of opposite sides is ___________.
- Sum of interior angles of a quadrilateral is ___________.
- A rectangle is a quadrilateral in which each of its angles is ___________.
- In a rhombus opposite ___________ are equal.
- Rhombus is a ___________ in which all its sides are equal.
- In a square all sides are ___________.
- A line segment which joins opposite vertices of a quadrilateral is called its ___________.
- Diagonals of a ___________ are equal in length.
- In a parallelogram, if one of its angles is 60° then its diagonally opposite angle must be ___________.
Write True or False Worksheet
| Type: | True False |
| Count: | 1 |
| S.N. | Statement | ✓ or ✕ |
|---|---|---|
| 1) | A quadrilateral has two diagonals. | |
| 2) | In isosceles trapezium, its base angles are equal. | |
| 3) | The diagonals of a parallelogram bisect each other at 90°. | |
| 4) | The diagonals of a rectangle bisect each other at 90°. | |
| 5) | The diagonals of a square bisect each other at 90°. | |
| 6) | The diagonals of a rhombus bisect each other at 90°. | |
| 7) | The diagonally opposite angles of a parallelogram are equal. | |
| 8) | The diagonally opposite angles of a rhombus are equal. | |
| 9) | The diagonals of a square are unequal in length. | |
| 10) | A parallelogram is a rhombus. |
Match Columns Worksheet
| Type: | Matching |
| Count: | 1 |
| 1) | Each angle of square is of measure | a) | parallel |
| 2) | Diagonals of rectangle are | b) | diagonals |
| 3) | Opposite sides of rhombus are | c) | congruent triangles |
| 4) | A quadrilateral has two | d) | equal |
| 5) | Sum of all angles of a rectangle is | e) | 90° |
| 6) | Diagonal divides a parallelogram into two | f) | 360° |
Multiple Choice Questions Worksheet
| Type: | MCQ |
| Count: | 1 |
- four sides
- five sides
- curve
- three sides
- four angles
- six angles
- three angles
- five angles
- Triangle
- Pentagon
- Rhombus
- Hexagon
- 1 right angle
- 2 right angle
- 3 right angle
- 4 right angle
- Square
- Rectangle
- Rhombus
- Isosceles trapezium
- Rectangle
- Square
- Rhombus
- Kite
- Rectangle
- Square
- Trapezium
- Rhombus
- Kite
- Rhombus
- Square
- Trapezium
- True
- False
- Maybe
- None of the above
- Square
- Kite
- Rhombus
- Parallelogram






























