Chapter Contents

Highest Common Factor with Properties & Methods to Find HCF

Maths Query > Unit > Arithmetic > Number System

Introduction

HCF or GCF (Greatest Common Factor) or GCD (Greatest Common Divisor), they all are the same terms. We use them while finding out the number which is the largest common divisor among many divisors of a number.
Let’s look at some general terms related to it and how it is calculated.

Factor of a number

A factor of a number is that number which divides the number exactly.

Example

What are the factors of 40?
There are a total of eight factors of 40 viz. 1, 2, 4, 5, 8, 10, 20 and 40.
Why?
∵ these all numbers give the remainder zero when 40 is divided by 1, 2, 4, 5, 8, 10, 20 and 40.
How?
⁴⁰₁ = 40
⁴⁰₂ = 20
⁴⁰₄ = 10
⁴⁰₅ = 8
⁴⁰₈ = 5
⁴⁰₁₀ = 4
⁴⁰₂₀ = 2
⁴⁰₄₀ = 1

Common factors of numbers

The factors which are common to two or more numbers are called common factors.

Example

Find the common factors of 4 and 10.
Step1: find out the factors of 4 and 10 separately.
Factors of 4:
⁴₁ = 4
⁴₂ = 2
⁴₄ = 1
There are a total of three factors of 4 viz. 1, 2 and 4.
Factors of 10:
¹⁰₁ = 10
¹⁰₂ = 5
¹⁰₅ = 2
¹⁰₁₀ = 1
There are a total of four factors of 10 viz. 1, 2, 5 and 10.
Step2: Find out the common factors of 4 and 10.
Finally, we can say 1 and 2 are the common factors of 4 and 10, because the factors 1 and 2 do exist for both numbers 4 and 10.

How to find greatest common factor?

There are three methods to find the greatest common factor.

Common factor method
Prime factorization method
Continued division method

Let’s learn them next with examples.

1. Common factor method

The number which is greatest among the common factors is called the highest common factor of two or more numbers.
So, what are the steps to find greatest common factor? Let’s learn them with an example.

Example

Find the GCF of 12 and 20.
Step 1: Find out the factors for 12.
Step 2: Find out the factors for 20.
Step 3: Find out the common factors of 12 and 20.
Step 4: Find out the greatest number among those common factors, that will be the GCF of 12 and 20.
Step1: Find out the factors for 12.
¹² = 12
¹²₂ = 6
¹²₃ = 4
¹²₄ = 3
¹²₆ = 2
¹²₁₂ = 1
There are a total of six factors of 12 viz. 1, 2, 3, 4, 6 and 12.
Step2: Find out the factors for 20.
²⁰₁ = 20
²⁰₂ = 10
²⁰₄ = 5
²⁰₅ = 4
²⁰₁₀ = 2
²⁰₂₀ = 1
There are a total of six factors of 20 viz. 1, 2, 4, 5, 10 and 20.
Step3: Find out the common factors of 12 and 20.
∴ the common factors are 1, 2 and 4.
Step4: Find out the greatest number among those common factors, that would be the GCF of 12 and 20.
∴ the greatest number among the common factors 1, 2 and 4 is 4.
Hence, GCF of 12 and 20 is 4.

2. Prime factorization method

This method considers common prime factors of given numbers to find the HCF. Let’s look at the steps used to find HCF with this method.

Step 1: Split each given number into its factors.
Step 2: Write the common prime factors obtained in step 2.
Step 3: Write the minimum number of times the each common prime factor occurs.
Step 4: Now multiply each common prime factor that obtained in last step.
This product of common prime factor obtained in step 4 is the required HCF.

Example

Example 1: Find the HCF of 12 and 20 using prime factorization method.
Step 1: Split 12 and 20 into its factors
12 = 2 × 2 × 3 = 2² × 3
20 = 2 × 2 × 5 = 2² × 5
Step 2: Write the common prime factors obtained in step 2.
Here, the common prime factor is 2.
Step 3: Write the minimum number of times the the common prime factor 2 occurs.
which is 2 times which is 2²
Step 4: Now multiply each common prime factor 2² that obtained in step 3.
2² = 2 × 2 = 4, which is the HCF of 12 and 20.

Example 2: Find the HCF of 84 and 48 using prime factorization method.
Step 1: Split 84 and 48 into its factors
84 = 2 × 2 × 3 × 7 = 2² × 3 × 7
48 = 2 × 2 × 2 × 2 × 3 = 2⁴ × 3
Step 2: Write the common prime factors obtained in step 2.
Here, the common prime factors are 2 and 3.
Step 3: Write the minimum number of times the the common prime factor 2 and 3 occur.
which is 2² and 3¹.
Step 4: Now multiply each common prime factor 2² and 3 that obtained in step 3.
2² × 3 = 4 × 3 = 12
∴ HCF of 84 and 48 is 12.

3. Continued division method

Continued division method or division method was developed by a Greek mathematician Euclid. So, it is also called as Euclid’s algorithm.
Let’s look at the steps used to find HCF using this method.

Step 1: Write the greatest number and the smallest number of the given numbers.
Step 2: Divide the greatest number by the smallest number.
Step 3: If the remainder is 0, then the smallest number is the required HCF, otherwise go to the next step.
Step 4: When remainder is not 0, then again divide the smallest number by obtained remainder. Continue doing the step 4 until remainder becomes 0.

Example

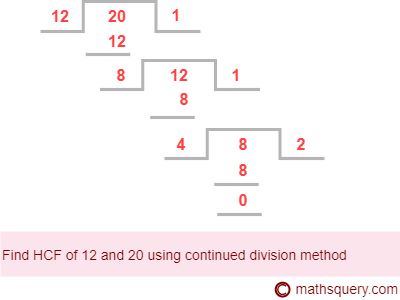
Example 1: Find HCF of 12 and 20 using division method.
Step 1: Write the smallest number and the largest number 12 and 20 respectively
Step 2: Divide the greatest number 20 by the smallest number 12.
Step 3: Now 8 is the remainder. If remainder in step 2 is 0, then the smallest number is HCF.
Step 4: Again divide the smallest number by the obtained remainder 8. Now, the remainder is 4. Continue doing the step 4 until remainder becomes 0.
Divide 8 by 4. Finally the remainder becomes 0.
Hence, HCF is 4.

Find HCF of 12 and 20 using continued division method

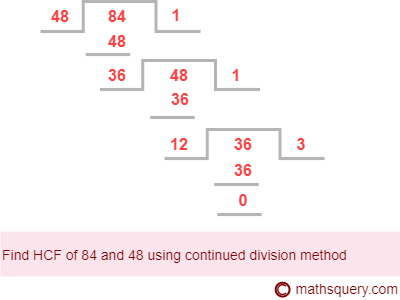
Example 2: Find HCF of 84 and 48 using division method.
Step 1: Write the smallest number and the largest number 48 and 84 respectively
Step 2: Divide the greatest number 84 by the smallest number 48.
Step 3: Remainder is 36. So, go to step 4.
Step 4: Again divide 48 by remainder 36. Now, the remainder is 12. Continue doing the step 4 until remainder becomes 0.
Divide 36 by 12 which gives the remainder 0.
Hence, HCF is 12.

Find HCF of 84 and 48 using continued division method

Five properties of greatest common divisor

Property 1

The GCD of two or more numbers exactly divides the numbers.

Example

GCD of two numbers 20 and 50 is 10.
It means the GCD 10 also divides the two numbers 20 and 50.

Property 2

The HCF of given numbers can’t be greater than its numbers.

Example

HCF of two numbers 27 and 60 is 3.
It means the HCF 3 can’t be greater than the two numbers 27 and 60

Property 3

If one number is factor of another number, the smaller number will be GCD.

Example

GCF of two numbers 27 and 54 is 27.
Here, 2 and 27 are factors of number 54. Also, 27 number is the number for which GCF will be calculated.
Therefore, GCF will be the smallest number of 27 and 54, which is 27.

Property 4

GCD of coprimes numbers is 1.

Example

GCD of 14 and 17 is 1.
Because, 14 and 17 are coprimes numbers.

Property 5

GCD of consecutive numbers is always 1.

Example

GCD of 19 and 20 is 1.
Because, 19 and 20 are consecutive numbers.

What is perfect number?

If the sum of all the factors of a number is two times the number itself, then the number is called a perfect number.

Example

6 is a perfect number
Why?
∵ sum of factors of 6 is 12
and 6 × 2 = 12
How?
Step1: Find out the factors of 6.
⁶₁ = 6
⁶₂ = 3
⁶₃ = 2
⁶₆ = 1
Factors of 6 are 1, 2, 3 and 6
Step2: Find the sum of factors
1 + 2 + 3 + 6 = 12
∴ we can see, the sum of factors of 6 which is 12 is equal to twice the number itself.

Frequently Asked Questions

1) What is highest common factor?

Highest common factor is the largest value of factor that can be obtained from the common factors of two or more given numbers.

2) What are the methods to find GCF?

There are three methods to find GCF. 1)Common Factor Method 2)PrimeFactor Method 3)Division Method

3) What is GCD?

The Highest Common Factor is also called as Greatest Common Divisor (GCD). It is also known by other name GCF (Greatest Common Factor).

Solved Examples

1) Find highest common factor of 70 and 85.

Factors of 70 are 1, 2, 5, 14, 35, 70.
Factors of 85 are 1, 5, 17.
From the above, the common factors of 70 and 85 are 1, 5.
Therefore, HCF 70 and 85 is 5.

2) Find greatest common factor of 14, 24 and 36.

Prime factors of 14 = 2 × 7
Prime factors of 24 = 2 × 2 × 2 × 3
Prime factors of 36 = 2 × 2 × 3 × 3
Common prime factor = 2
∴ HCF of 14, 24 and 36 = 2