Add numbers using number line
Let’s understand first what a number line is. It is a straight line with marked numbers on it at equal distances. The numbers on a number line start from left from 0 and increase towards the right side. It is like the one shown shown as below.

Steps to add numbers on number line
Step 1: To add two numbers, take the first number. Start from 0 on number line and move to the
right until you reach the given number.
Step 2: Take the second number. On the number line, start from the first number drawn on number line.
Jump to the right one by one by number of steps equal to the second number.
Add 14 and 5 using number line.
To add 14 and 5, draw a number line from 0 to 20.

Step 1:Start from 0 on number line then move to the right until we reach 14, which is the first number.

Step 2: Take second number 5, jump to the right one by one by 5 steps the second number.

Finally, after jumping by 5, we reach 19, which is the answer of sum of 14 and 5.
∴ 14 + 5 = 19
Downward addition of numbers
In this method, the numbers are added up after arranging the numbers in order of places like ones, tens, hundreds, thousands and so on. Let’s first take a short look at what are the places in a number
The digits in a number have their own positions namely ones, tens, hundreds, thousands and so on which are called places. These places start from the digit which is at the very right end of the number and moves from right to left. The digit which is at the rightmost side in a number is at place “Ones” and second from right is at “Tens”. Following is the chart to know the different place names in a number written in an increasing order from right to left.
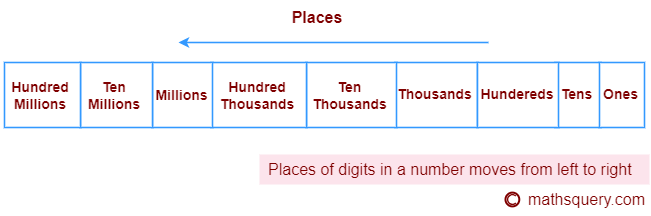
The places of the digits in a number 4936 are 6 at ones place, 3 at tens place, 9 at hundreds place and 4 at thousands place. They can be easily understood from the following figure also.

How to know place and place value of a digit in a number have been explained with examples in the chapter Digit, Face, Place Values and Comparison of Numbers.
Steps to add numbers downwards
Following steps can be used to add numbers downward.
Step 1: Write all the given numbers in an order of places of ones, tens, hundreds, thousands and so
on.
Step 2: Add all digits under a same place in downward direction starting from first column or ones
place to the second column or tens place and so on.
Let’s understand it with an example.
Add the numbers 14 and 25
Step 1: Write 4 under ones place and 1 under tens place from 14. Write 5 under ones place and 2 under tens place from 25.

Step 2:
Add all digits at ones place i.e. 4 and 5. So, 4 + 5 = 9.

Also, add all digits at tens place i.e. 1 and 2.
So, 1 + 2 = 3.

So, addition of 14 and 25 is equal to 39.
Addition of numbers with carryover
When adding numbers, there may be a case when the sum of two digits in a column is
more than 9, eventually a 2 digit number.
In such cases, the digit at tens place of the sum carried over to the next column.
Then the carried over digit is added up to the rest of the digits in that column.
In the above example of adding 14 and 25, the sum of first column digits 4 and 5 is 9, which means it is
less than 9, so this example is without any carryover digit.
Steps to add numbers with carryover
Step 1: Write the 3 digits numbers at their ones, tens and hundreds places
Step 2: Add the digits at each place starting from ones and moving to tens then hundreds and so on.
If at any place, the total of digits obtained is more than 9 then the digit at tens place of the total is
carried
over to the next upper place. This carried over digit is added up to the rest of digits at that place of given numbers.
Lat’s take an example to add three digit numbers with carryover.
Add 386 and 978
Step 1: Write the 3 digits numbers 386 and 978 at their ones, tens and hundreds places.

Step 2:
Add the digits of first column or at ones place i.e. 6 and 8. So, 6 + 8 = 14.
Now, 14 is a two digit number. So, here, 1 is at tens place, which is a carryover digit. Write
the carryover 1 at the top of tens place digits or second column i.e. 8 and 7.

Add all digits at tens place i.e. 1, 8 and 7. So, 1 + 8 + 7 = 16.
Again, 16 is a two digit number. So, write the carryover 1 at the top of hundreds place digits or
third column i.e. 3 and 9.

Add all digits at hundreds place i.e. 1, 3 and 9. So, 1 + 3 + 9 = 13.
The total 13 of last place digits i.e. 1, 3 and 9, is written as it is.

So, addition of 386 and 978 is equal to 1364.
Subtract numbers using number line
Step 1: To subtract two numbers, on the number line first locate the largest number out of the two
numbers after starting from 0.
Step 2: Start from the first number drawn on number line in step 1. Locate the smallest number on
number line by jumping to the left direction from the largest number by one step at a time.
The last number reached on the number line will be the answer of the subtraction.
Subtract 4 from 10 using number line.
Step 1: Locate the largest number 10 after starting from 0 on number line.

Step 2: Starting from 10 jump back in the left direction one step at a time until reached to 4.
After moving 4 steps to left, finally the number reached on number line is 6.

So, 6 is the answer of subtraction of 4 from 10.
∴ 10 – 4 = 6
Downward subtraction of numbers
In this method, the smallest number is subtracted from the largest number after arranging them at their correct places. The steps to subtract numbers downward are as following:
Step 1: First write the largest number and the smallest number below it in the order of places of
ones, tens, hundreds, thousands and so on.
Step 2: Start subtracting digits which are at the same place in downward
direction from the right side and move towards left.
Subtract 12 from 35
Step 1: Write 4 under ones place and 1 under tens place from 14. Write 5 under ones place and 2 under tens place from 25.

Step 2:
Add all digits at ones place i.e. 4 and 5. So, 4 + 5 = 9.

Also, add all digits at tens place i.e. 1 and 2.
So, 1 + 2 = 3.

So, addition of 14 and 25 is equal to 39.















