What is an Angle, its Measures and Types of Angle?

Introduction

In the chapter Point, Line, Ray, Line Segment and Plane we learnt about the basic geometrical concepts of rays. The inclination of these rays to each other leads to the formation of an angle. The word “angle” originates from the latin word which is “angulus”, which means in latin as corner.

In daily life we can see an example of angle formation when a ladder is leaned against a wall. In such scenario of leaned ladder against the wall, the angle is formed at top of the ladder where ladder and wall meet at a point and the second angle is formed where ladder and floor meet at a point.

Let’s take a deep look at the basics of angle, its measurements and various types.

What is an Angle?

A figure formed by joining two different rays starting from the same fixed initial point is called an angle.

Example of an angle ∠AOB

In the given figure, this figure is made up of two rays OA and OB . The common end point of two rays is called the vertex of the angle.
So, O is the vertex of angle AOB.
The rays OA and OB are called the arms or sides of angle AOB.
An angle is denoted by the symbol ∠.
Only capital letters of English alphabets are used to name an angle. Name of angles can be written using three or one alphabet.
Thus, we can write the above angle in figure as ∠AOB or ∠BOA or ∠O.
We can see from the naming that vertex is always kept at the centre when written using three alphabets and only vertex when written as a single alphabet.

Measurement of angle

The unit of measuring an angle is degree.
The word degree originates from the Latin word “gradius” which means “step”. It refers to a stage in an ascending or descending order.
The symbol used for degree is “°”. It is inserted on the right top of the numeral.
for example, 90 degrees = 90°

Types of angle

1. Acute angle

An angle which is less than 90°, is called acute angle.

Example of Acute angle

2. Right angle

An angle which is equal to 90°, is called right angle.

Example of Right angle

3. Obtuse angle

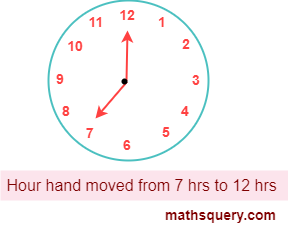
An angle which is greater than 90° and less than 180° is called obtuse angle.

Example of Obtuse angle

4. Straight angle

An angle which is equal to 180°, is called straight angle or straight line angle.

Example of Straight angle

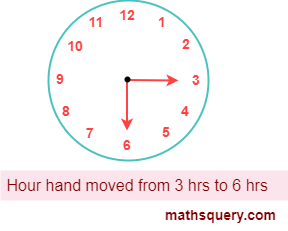
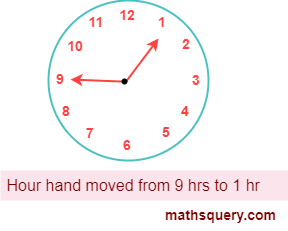
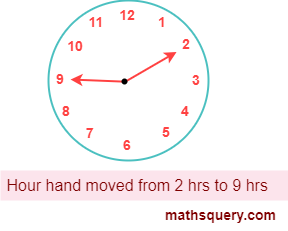
5. Reflex angle

An angle which measure greater than 180° but less than 360° is called reflex angle.

Example of Reflex angle

6. Complete angle

An angle is said to be complete angle if two different rays coincide with initial point after making a complete revolution.

Example of Complete angle

Here, ray OA and ray OB coincide each other after making a complete revolution.
∠AOB = 360°

7. Zero angle

An angle is said to be zero angle if two different rays coincide without any revolution.

Example of Zero angle

Here, ray OA and ray OB coincide ∠AOB
∠AOB = 0°

Note

The acute and obtuse angles are known as oblique angles.

What are Congruent angles?

Angles having the same measure are said to be congruent angles.

Example of Congruent angles

What are Adjacent angles?

Two angles are said to be adjacent angles if they have common vertex, a common arm and other two arms of the angles are on the opposite sides of the common arm.

Example of Adjacent angles

In the given figure, two angles ∠AOB and ∠BOC have a common arm OB, a common vertex O and the other two arms OA and OC lie on the opposite sides of common arm OB.

1. Complementary angles

Two angles are said to be complementary if they form adjacent angle and sum of their measure is equal to 90°

Example of Complementary angles

∠AOC + ∠BOC
= 45° + 45°
90°

2. Supplementary angles

Two angles are said to be supplementary angles if they form adjacent angles whose sum of their angles is equal to 180°

Example of Supplementary angles

∠ABO + ∠CBO
=120° + 60°
180°

List of types of angles with measures

Name of angle	Measure
Acute angle	0^° < θ < 90^°
Right angle	θ = 90^°
Obtuse angle	90^° < θ < 180^°
Straight angle	θ = 180^°
Reflex angle	180^° < θ < 360^°
Complete angle	θ = 360^°
Zero angle	θ = 0^°

Solved Examples

1) Classify the following as acute, obtuse, right angle, complete angle and reflex angle.

27°
110°
180°
232°
360°
180 ^{3^°} ₄

27°
As 27° lies between 0° and 90°, it is an acute angle.
110°
110° is an obtuse angle because it lies between 90° and 180°.
180°
180° is a straight angle.
232°
232° is a reflex angle because it lies between 180° and 360°.
360°
360° is a complete angle.
180 ^{3^°} ₄
180 ^{3^°} ₄ =180.75° lies between 180° and 360°.

2) Find the angle formed by an hour hand of a clock when it moves:

from 3 to 6
from 12 to 6
from 9 to 1
from 7 to 12
from 2 to 9

from 3 to 6

Number of hours when hour hand moves from 3 to 6 = 3 hours.
An hour hand forms 360° angle when it moves once cycle starting from 12 and ending at 12 on a clock. Or we can say, an hour hand makes 360° angle in 12 hours.
Or, angle formed in 12 hours = 360°
∴ angle formed in 1 hour = ³⁶⁰ ₁₂
So, angle formed in 3 hours = ³⁶⁰ ₁₂ × 3
= 90°
= 1 right angle
from 12 to 6

Number of hours when hour hand moves from 12 to 6 = 6 hours.
Angle formed by hour hand in 12 hours = 360°
angle formed in 1 hour = ³⁶⁰ ₁₂
So, angle formed in 6 hours = ³⁶⁰ ₁₂ × 6
= 180°
= a straight angle
from 9 to 1

Number of hours when hour hand moves from 9 to 1 = 4 hours.
Angle formed by hour hand in 12 hours = 360°
angle formed in 1 hour = ³⁶⁰ ₁₂
So, angle formed in 4 hours = ³⁶⁰ ₁₂ × 4
= 120°
from 7 to 12

Number of hours when hour hand moves from 7 to 12 = 5 hours.
Angle formed by hour hand in 12 hours = 360°
angle formed in 1 hour = ³⁶⁰ ₁₂
So, angle formed in 5 hours = ³⁶⁰ ₁₂ × 5
= 150°
from 2 to 9

Number of hours when hour hand moves from 2 to 9 = 7 hours.
Angle formed by hour hand in 12 hours = 360°
angle formed in 1 hour = ³⁶⁰ ₁₂ × 6
So, angle formed in 7 hours = ³⁶⁰ ₁₂ × 7
= 210°

3) Out of east, west, north and south in which direction will a man be after starting a walk towards west, then taking a turn of ¹ ₂ revolution in clockwise direction.

Example of angle calculation of a man moving in west direction then turns clockwise

1 revolution = 360°
¹ ₂ revolution = ¹ ₂ × 360 = 180°
So, the man started walking in west direction and takes a turn of ¹ ₂ revolution which will be 180° in clockwise direction.
From the diagram, the east direction is at 180° of west direction in clockwise.
So, the man finally will be moving towards east direction.

4) Out of east, west, north and south in which direction will a man be after starting a walk towards north, then taking a turn of ³ ₄ revolution in anticlockwise direction.

Example of angle calculation of a man moving in north direction then turns anticlockwise

1 revolution = 360°
³ ₄ revolution = ³ ₄ × 360 = 270°
So, the man started walking in north direction and takes a turn of ³ ₄ revolution which will be 270° in anti clockwise direction.
From the diagram, the west direction is at 270° of north direction in anticlockwise.
So, the man finally will be moving towards west direction.

Fill in Blanks Worksheet

Type:	Blanks
Count:	1

The measure of one complete angle is equal to four ___________ angles.
An angle of 180° measure is called ___________.
The common initial point of two rays is called as ___________.
An angle whose measure is greater than that of the right angle but less than 180° is ___________.
The two intersecting rays at a point form an angle, the two rays are called as ___________ of the angle.
The measure of 2 right angles is ___________.
The sum of two angles is 90°, then each of them is ___________ angle.
At 7 o'clock, the angle formed between minute hand and hour hand is a ___________ angle.
At 12 o'clock, the angle formed between minute hand and hour hand is ___________.
¹ ₂ of straight angle is equal to ___________.