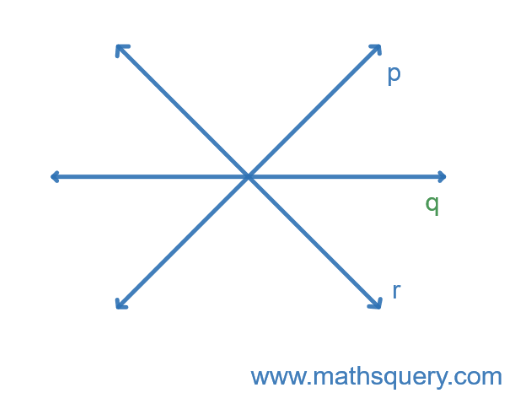Point, Line, Ray, Line Segment and Plane

Introduction

A point and a line are considered as one of the most fundamental building blocks of geometry. A line segment, a ray and a plane are the geometrical objects which can not be drawn without the help of a point and line.

This chapter discusses the definitions and examples of point, line, ray, line segment and a plane. How two or more than two lines can make when meet at some point for example intersecting lines, perpendicular lines, parallel lines, transversal lines and concurrent lines with the help of diagrams. FAQs, Solved Examples and MCQs related to points, lines, rays, line segments and planes have been given at the end of the chapter to go through the example questions and to practice more questions.

Point in Geometry

In geometry, when we mark the exact position of an object with a dot, that is called a point. It has no length and breadth. Also, it occupies no depth. In other words, a point determines a location.
It is denoted by a dot “∙” symbol.
We use capital letters of alphabets to name a point.

Two points A and X

Line in Geometry

A Line is a one dimensional figure which is straight, has indefinite length and no thickness. Line can be extended indefinitely only in two directions which are opposite to each other. A line has an infinite number of points lying on it.
A line has no end points.
We can name the lines by using two capital letters of alphabets and an arrow that points in both directions.

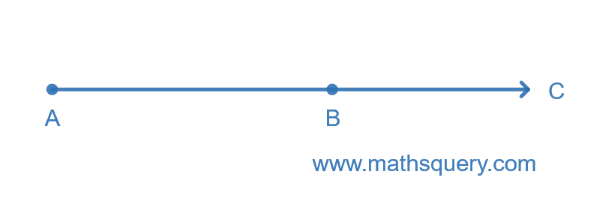
Line AB

What is a Ray in Geometry?

It is a straight line which starts from one fixed point and always progress in one direction only away from that starting point. Ray can be extended indefinitely only in one direction.
It has one end point. It has no definite length and can’t be measured.
Ray is represented by two capital letters of alphabets with a pointed arrow on top of it.

Ray AB

What is a Line Segment in Geometry?

A Line segment is a part or segment of a line that is bounded by two distinct end points those lie on that line. A Line segment has a number of other points lying on it, but they all lie in between the two end points only.
Line segment is also represented by two capital letters of alphabets but with a line on top of it.

Line segment AB

Plane in geometry

In geometry, a plane is a flat and smooth surface. It has length and width. It has no thickness. Plane can be extended indefinitely in all directions.

Example of a Plane

We can name the plane by using English alphabets. For example, the plane drawn in the above diagram can be named with letters A, B and C and called as Plane ABC.

Another example of a Plane

This plane can be named with letters P, Q, R and S and called as Plane PQRS.
The real life examples of a plane, that can we see around us and everywhere are surface of a wall and ceiling of a room.

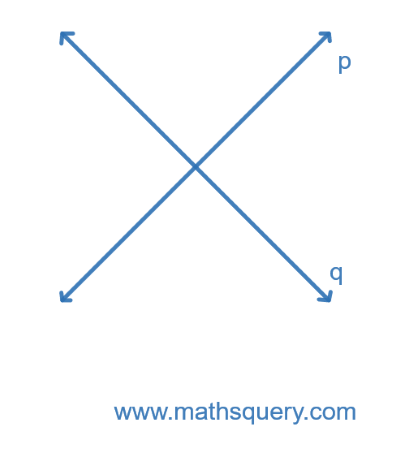
What are Intersecting lines?

Two lines are said to be intersecting lines if they meet out at a point.

Intersecting lines AB and CD

Line AB and line CD intersect each other at a point E.

What are Perpendicular lines?

The lines are said to be perpendicular lines if they intersect each other and the angle between them is 90°.

Perpendicular lines AB and CD

Lines AB and CD intersect at O and form an angle of 90° in each quadrant.
Line AB is perpendicular to line CD. To denote AB is perpendicular to CD, we use symbol ⊥.
So, we can write it as AB ⊥ CD or we can write as CD ⊥ AB.

What are Parallel lines?

Two straight lines are said to be parallel lines if they do not intersect each other at any point although we extend these line in both directions indefinitely.

Parallel lines AB and CD

Line AB is parallel to CD. To denote it, we can use symbol ||. So. it is written as AB||CD or CD||AB.

What is a Transversal line?

A line is said to be a transversal line, if it cuts two or more lines at different points and those lines can be parallel or non parallel lines.

Transversal lines AB and CD

Here, line AB cuts through two lines PQ and RS where line AB is called as transversal line.

What are Concurrent lines?

If three or more straight lines pass through the same point or intersect each other at same point, then these lines are called concurrent lines.
The point where lines intersect each other, is called point of concurrence.

Concurrent lines AB, CD, PQ and RS

Here, AB, CD, PQ and RS are concurrent lines, as these lines pass through the same point T. T is called the point of concurrence.

What are collinear points?

If three or more points lie on the same straight line then points are called collinear points.

Collinear points A, B, C and D on a line

Here, A, B, C and D are collinear points as they lie in the same straight line.