Introduction
We have learnt earlier in the chapter Polynomial, its Terms, Degree and Types, the meaning of polynomials and its various types. This chapter is about what are zeros of polynomials, understand the zeros of polynomials graphically and finding the value of zeros of polynomial graphically for a linear polynomial, a cubic polynomial and a biquadratic polynomial.
Let’s first understand what are zeros of a polynomial. We can represent a polynomial on graph with a curve which intersects the axis at specific points. The values of the intersecting points on the x-axis are the values that make the polynomial equal to zero. These points on the x-axis which make a polynomial equal to zero are called zeros of a polynomial.
Below is an example of a polynomial which is drawn as a curve on a graph.

In this graph, the curve of polynomial y = x + 4 intersects the x-axis at x = – 4 and y-axis at y = 4 or the
intersecting points on the x-axis for x = -4 is (-4,0) and and on the y-axis for y = 4 is (0,4).
As said above in the introduction, the values of x that lie on x-axis i.e. x = -4 is the zero of the
polynomial.
How?
We can check it by putting the value of x = – 4 in the polynomial y = x + 4, if y comes equal to 0 for x =
-4, then the value of x is zero of the polynomial.
Substitute value x = – 4 in polynomial y = x + 4.
y = (-4) + 4
y = -4 + 4
y = 0
∴ x=-4 is zero of the polynomial.
Definition
A real number k is the zero of polynomial p(x) if p(k)= 0.
Let’s see what it says. If p(x) is a polynomial in x and k is any real number, then value obtained by
replacing x by k in p(x) is called the value of p(x) at x = k and is denoted by p(k).
If the value of k in a polynomial can make the value of polynomial to zero, then k is called zeros of
polynomial.
We can learn it by example, how we can find out the zeros of a polynomial.
Zeros of a polynomial are determined by putting different value of x, which can make value of polynomial to
0.
Find zeros of polynomial p(x) = x2 – 5x + 6
p(x) = x2 – 5x + 6
Put value x = 2
p(2) = (2)2 – 5(2) + 6
= 4 – 10 + 6
= 10 – 10
= 0
p(2) = 0
∴ 2 is zero of polynomial p(x)
Put value x = 3
p(3) = (3)2 -5(3) + 6
= 9 – 15 + 6
= 15 – 15
= 0
∴ 3 is also zero of polynomial p(x)
So, 2 and 3 are two zeros of polynomial p(x).
Geometrical meaning of zeros of polynomial
Any polynomial can be drawn on a graph with a specific curve. We have already introduced above in Introduction section how the polynomial curves are drawn on a graph. The shapes of the curves of polynomial varies with polynomial degree. Linear polynomial has curves of unique shape and are different from quadratic polynomial and even biquadratic has its own unique shape. Let’s learn what are the shapes and how to find zeros of polynomials for linear, quadratic, cubic and biquadratic polynomials.
Linear polynomial
The general form of a linear polynomial is ax + b, where a ≠ 0. The graph of linear polynomial is a straight line and it intersects the x-axis at exactly one point. So, the linear polynomial has only one zero.
Consider a linear polynomial, y = 2x + 6
To find the zeros, we put y = 0
2x + 6 = 0
x = -3
∴ -3 is zero of y = 2x + 6 linear polynomial

Quadratic polynomial
The general form of a quadratic polynomial is ax2 + bx + c, where a ≠ 0. The graph of quadratic polynomial has two shapes, one is known as open upwards or in shape of ∪ and another is open downwards or in shape of downwards ∩. These curves are also called parabolas. Let’s find zeros of a quadratic polynomial in an example as below.
Consider a quadratic polynomial, y = x2 + 2x – 3
To find zeros of a polynomial, let’s start by putting the value of x and find the corresponding y.
Put x = 0
y = (0)2 + 2(0) – 3
y = 0 + 0 – 3
y = 0 – 3
y = -3
Put x = -3
y = (-3)2 + 2(-3) – 3
y = 9 – 6 – 3
y = 9 – 9
y = 0
Put x = 1
y = (1)2 + 2(1) – 3
y = 1 + 2 – 3
y = 3 – 3
y = 0
The zeros of quadratic polynomial x2 + 2x – 3 will be the x coordinates of points where
the graph
y = x2 + 2x – 3 intersects the x-axis.
Therefore, -3 and 1 are zeros of polynomial x2 + 2x – 3 as graph y = x2 + 2x –
3 intersects x-axis at -3 and 1.

Therefore, for quadratic polynomial ax2 + bx + c, a ≠ 0, zeros of polynomial are
x-coordinates of
points
where the parabola y = ax2 + bx + c intersects the x-axis.
Further, for the graph of y = ax2 + bx + c, there are three cases that arises with different
shapes of graph.
Let’s have a look at it one by one.
Graph of a quadratic polynomial with distinct zeros
First case of a graph is when the graph cuts the x-axis at two distinct points A and B. The x-coordinate of A and B are two zeros of the quadratic polynomial ax2 + bx + c.

Graph of a quadratic polynomial with coincident zeros
The graph of the polynomial ax2 + bx + c cuts the x-axis at exactly one point i.e. at two coincident points. So the two points A and B coincide here to become one point A. The x-coordinates of A is only one zero for quadratic polynomial ax2 + bx + c.

Graph of a quadratic polynomial with no zeros
Here the graph is completely above x-axis and completely below x-axis. It does not cut the x-axis at any point. So, the quadratic polynomial has no zero in this case.

Therefore, we can summarise from the above three cases, geometrically, a quadratic polynomial can have either two distinct zeros or two equal zeros or no zero. In other words, a quadratic polynomial can have at most two zeros.
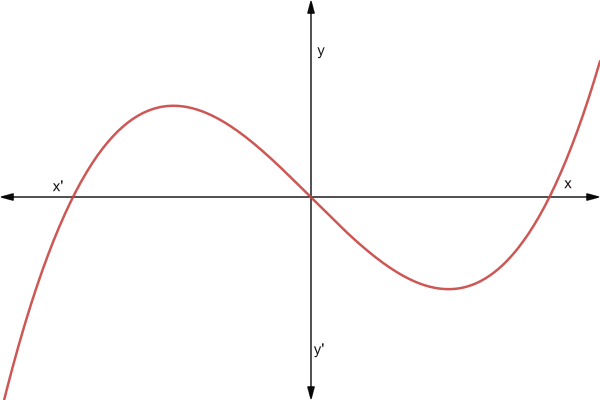
Cubic polynomial
The general form of a cubic polynomial is ax3 + bx2 + cx + d, where a ≠ 0. The
graph of cubic
polynomial
intersects the x-axis at points, the coordinates of these points are the only zeros of the cubic polynomial.
Let’s find zeros of a cubic polynomial in an example as below.
Consider a cubic polynomial, y = x3 – x
To find zeros of a polynomial, let’s start by putting the value of x and find the corresponding y.
Put x = 1
y = (1)3 – (1)
y = 1 – 1
y = 0
Put x = 0
y=(0)3 – (0)
y = 0 – 0
y = 0
Put x = -1
y = (-1)3 – (-1)
y = -1 + 1
y = 0
Put x = -2
y = (-2)3 – (-2)
y = -(-8) + 2
y = -6
The zeros of cubic polynomial y = x3 – x will be the x coordinates of points where the
graph
y = x3 – x intersects the x-axis.
Here 1, 0 and -1 are zeros of cubic polynomials as these are points where the graph intersects the
x-axis.

Biquadratic polynomial
The general form of a biquadratic polynomial is ax4 + bx3 + cx2 + dx + c,
where a ≠ 0. The graph of
biquadratic polynomial intersects the x-axis at points, the coordinates of these points are the only zeros of
the biquadratic polynomial.
Let’s find zeros of a biquadratic polynomial in an example as below.
Consider a biquadratic polynomial,
y = x4 – 6x3 – 4x2 + 54x – 45
To find zeros of the polynomial, let’s start by putting the value of x and find the corresponding y.
Put x = -3
y = (-3)4 – 6(-3)3 – 4(-3)2 + 54(-3) – 45
y = (81) – 6(-27) – 4(9) – 162 – 45
y = 81 + 162 – 36 -162 – 45
y = 0
Put x = 1
y = (1)4 – 6(1)3 – 4(1)2 + 54(1) – 45
y = 1 – 6 – 4 + 54 – 45
y = 0
Put x = 3
y = (3)4 – 6(3)3 – 4(3)2 + 54(3) – 45
y = 81 – 162 – 36 + 162 – 45
y = 0
Put x = 5
y = (5)4 – 6(5)3 – 4(5)2 + 54(5) – 45
y = 625 – 750 – 100 + 270 – 45
y = 0
The zeros of cubic polynomial y = x4 – 6x3 – 4x2 + 54x – 45 will be
the x coordinates of points where the
graph y = x4 – 6x3 – 4x2 + 54x – 45 intersects the x-axis.
Here, -3, 1, 3 and 5 are zeros of biquadratic polynomial as these are points where the graph intersects
x-axis.