Introduction
Cartesian Coordinate System is used to describe the position of a point in a plane using
coordinates in coordinate geometry. Coordinates are the way of telling the position of a point using numbers.
Rene Discartes
invented
the Coordinate System and the term Cartesian Coordinate System is named after the name of Discartes
mathematician to honour the inventor.
Cartesian geometry system introduces coordinate axes, coordinates and quadrants to describe
the position of a point in a plane and its distances from other points.
Let’s learn about these new terms next.
Coordinate axes
Cartesian coordinate system uses a plane which has two mutually perpendicular lines which are called as coordinate axes. Out of the two perpendicular lines, one line is in horizontal position and another line is in vertical position. The figure below shows how the two coordinate axes look like.
Mind the words axis and axes, how they are used. Axis is used to represent one axis, it is singular. On the other hand, axes is used to represent more than one axis, which is plural.


The horizontal line marked with XX‘ is called as x-axis and vertical line marked as YY‘ is called as y-axis. Both axes, x-axis and y-axis intersect each other at point O and are perpendicular to each other. The point O is called as origin.
Directions of axes
So, x-axis has two sides, one side lies on right side of y-axis and can be read as OX. The second side lies on
left side of y-axis and is read as OX‘. Similarly, y-axis has two sides top and bottom of x-axis. The
top side of y-axis is read as OY and bottom side of y-axis is OY’.
The OX on x-axis and OY on y-axis called as
positive directions of x-axis and y-axis respectively. Similarly, the OX‘ on x-axis and
OY‘ on y-axis called as negative directions of x-axis and y-axis respectively.

Scaling of axes
Scaling of axes is meant by marking the x-axis and y-axis with numbers which are placed at equal distances. The
ray OX on x-axis has positive numbers (1, 2, 3, 4, ….) and ray OX‘ has negative numbers (-1, -2,
-3, -4, ….) only. Similarly,
The ray OY on y-axis has positive numbers (1, 2, 3, 4, ….) and ray OY‘ has negative numbers (-1,
-2, -3, -4, ….) on it.
In other words, we can say that positive numbers lie in the directions of ray OX and ray OY and the negative
numbers lie
in the direction of ray OX‘ and ray OY‘.
Quadrants
The two coordinate axes x-axis and y-axis in coordinate geometry divide the plane into four parts. These four parts are called as quadrants.

In above figure, x-axis and y-axis is dividing the plane into four parts which are XOY, X‘OY,
X‘OY‘ and XOY‘.
XOY is called as first quadrant.
X‘OY is called as second quadrant.
X‘OY‘ is called as third quadrant.
XOY‘ is called as fourth quadrant.
Also, the four quadrants are numbered as I, II, III and IV anticlockwise starting from first quadrant XOY and
the last quadrant as X‘OY‘.
Coordinates of a point
Any point in a plane can lie in any of the four quadrants I, II, III or IV. The position of a point is in the
plane is called as coordinates of that point. Coordinates of the point in a quadrant is determined by
knowing
its perpendicular distances from its nearest x-axis and y-axis.
Coordinates of a point is written by writing its perpendicular distance in brackets in the format of (x,y),
where x is the perpendicular distance of the point from x-axis and y is the perpendicular distance of the point
from y-axis.
The x-axis coordinate of a point is called as abscissa.
The y-axis coordinate of a point is called as ordinate.
Coordinates of a point can be written only in specific order i.e (x,y). First we write abscissa followed by
ordinate and seperated by a comma.
Abscissa and ordinate of a point cannot be interchanged.
i.e. (x,y) ≠ (y,x)
Moreover, (x,y) = (y,x) if x = y
Let’s take an example to understand it precisely

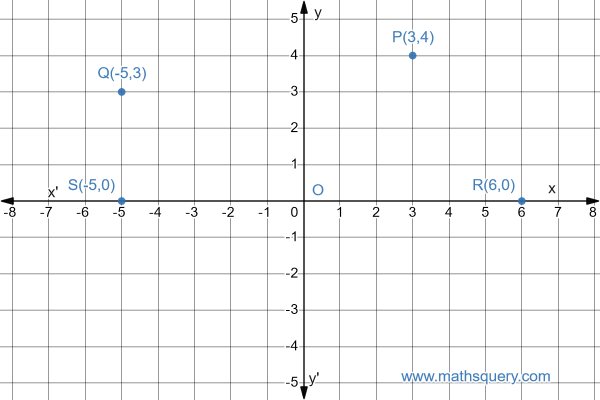
From the above figure, we can see
P is the point that lie in first quadrant and is marked has P.
The perpendicular distance PN of point P from y-axis is 3 units, measured along the positive direction
of x-axis as OM which is 3 units.
The perpendicular distance PM of point P from x-axis is 4 units, measured along the positive direction
of y-axis as ON which is 4 units.
So, the perpendicular distance of point P from y-axis is 3 and x-axis is 4, so the coordinate of the point P
can be written as (3,4).
Coordinates of origin are always written as (0,0) because perpendicular distance of origin from x-axis is zero and from y-axis is also zero.
The ordinate of any point on x-axis is 0 i.e coordinate of any point on x-axis is (x,0).
The abscissa of any point on y-axis is 0 i.e coordinate of any point on y-axis is (0,y).
Sign conventions in quadrants
As we have read above, the x-axis XOX’ and y-axis YOY’ divide the coordinate plane into four quadrants.
The ray OX is regarded as positive x-axis.
The ray OY is regarded as positive y-axis.
The ray OX‘ is regarded as negative x-axis.
The ray OY‘ is regarded as negative y-axis.
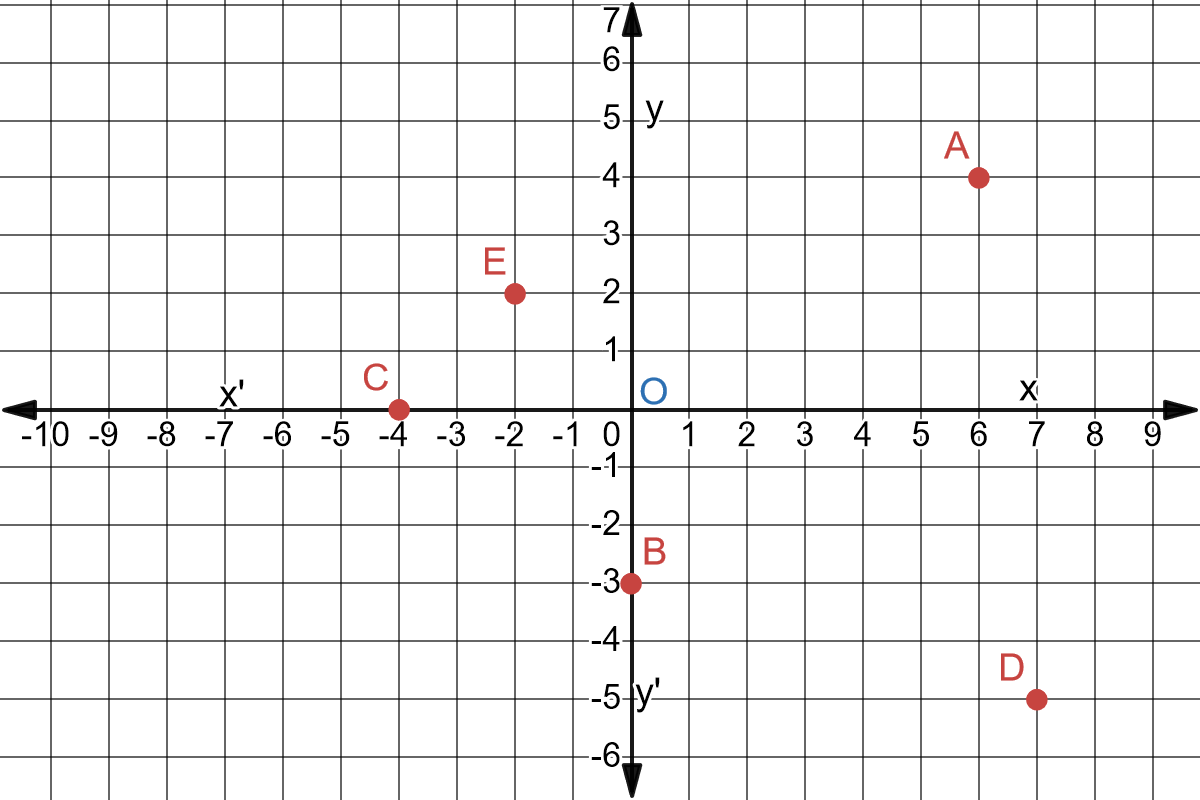
So, any point that lies in first quadrant will always have positive abscissa and positive ordinate.
Any point that lie in second quadrant has negative abscissa and positive ordinate.
Any point that lie in third quadrant has negative abscissa and negative ordinate.
Any point that lie in fourth quadrant has positive abscissa and negative ordinate.
Please refer to the following figure, how the signs of abscissa and ordinate looks like in the four
quadrants.

So, In the figure:
first quadrant has points with sign (+,+).
second quadrant has points with sign (-,+).
third quadrant has points with sign (-,-).
fourth quadrant has points with sign (+,-).